题目内容
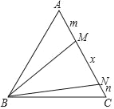
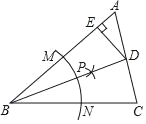
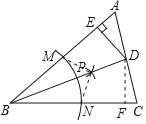
【题目】如图所示,在△ABC中:
(1)下列操作中,作∠ABC的平分线的正确顺序是怎样(将序号按正确的顺序写出).
①分别以点M、N为圆心,大于![]() MN的长为半径作圆弧,在∠ABC内,两弧交于点P;
MN的长为半径作圆弧,在∠ABC内,两弧交于点P;
②以点B为圆心,适当长为半径作圆弧,交AB于点M,交BC于N点;
③画射线BP,交AC于点D.
(2)能说明∠ABD=∠CBD的依据是什么(填序号).
①SSS.②ASA.③AAS.④角平分线上的点到角两边的距离相等.
(3)若AB=18,BC=12,S△ABC=120,过点D作DE⊥AB于点E,求DE的长.
【答案】(1)作∠ABC的平分线的正确顺序是②①③;(2)①;(3)DE=8.
【解析】
(1)根据基本作图方法即可得出;
(2)证明△MBP≌△NBP即可;
(3)过点D作DF⊥BC与F,由题意推出DE=DF,再由S△ABC=S△ABD+S△CBD即可求出DE的长度.
(1)作∠ABC的平分线的正确顺序是②①③,
故答案为:②①③;
(2)在△MBP和△NBP中,
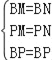 ,
,
∴△MBP≌△NBP(SSS),
∴∠ABD=∠CBD,
故答案为:①;
(3)过点D作DF⊥BC与F,
∵∠ABD=∠CBD,DE⊥AB,DF⊥BC,
∴DE=DF,
S△ABC=S△ABD+S△CBD,即![]() ×AB×DE+
×AB×DE+![]() ×BC×DF=120,
×BC×DF=120,
∴![]() ×18×DE+
×18×DE+![]() ×12×DE=120,
×12×DE=120,
解得,DE=8.

练习册系列答案
相关题目