题目内容
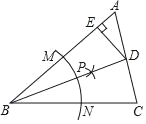
【题目】如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为( )
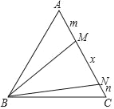
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 随x,m,n的值而定
【答案】C
【解析】
将△ABM绕点B顺时针旋转60°得到△CBH.连接HN.想办法证明∠HCN=120°HN=MN=x即可解决问题.
将△ABM绕点B顺时针旋转60°得到△CBH.连接HN.
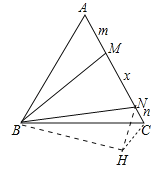
∵△ABC是等边三角形,∴∠ABC=∠ACB=∠A=60°.
∵∠MON=30°,∴∠CBH+∠CBN=∠ABM+∠CBN=30°,∴∠NBM=∠NBH.
∵BM=BH,BN=BN,∴△NBM≌△NBH,∴MN=NH=x.
∵∠BCH=∠A=60°,CH=AM=n,∴∠NCH=120°,∴x,m,n为边长的三角形△NCH是钝角三角形.
故选C.

【题目】借助表格进行多项式乘多项式运算,可以方便合并同类项得出结果.下面尝试利用表格试一试.
例题:(a+b)(a﹣b)
解填表
| a | b |
a | a2 | ab |
﹣b | ﹣ab | ﹣b2 |
则(a+b)(a﹣b)=a2﹣b2.
根据所学完成下列问题.
(1)如表,填表计算(x+2)(x2﹣2x+4),(m+3)(m2﹣3m+9),直接写出结果.
| x2 | ﹣2x | 4 |
x | x3 | ﹣2x2 | 4x |
+2 | 2x2 | ﹣4x | 8 |
| m2 | ﹣3m | 9 |
m | m3 | ﹣3m2 | 9m |
+3 | 3m2 | ﹣9m | 27 |
结果为 ;结果为 .
(2)根据以上获得的经验填表:
| |||
△ | △3 | ||
〇 | 〇3 |
结果为△3+〇3,根据以上探索,请用字母a、b来表示发现的公式为 .
(3)用公式计算:(2x+3y)(4x2﹣6xy+9y2)= ;
因式分解:27m3﹣8n3= .
【题目】小明买了张100元的乘车IC卡,如果他乘车的次数用x表示,则记录他每次乘车后的余额y元)如表:
次数x | 1 | 2 | 3 | 4 | … |
余额y | 100-1.2 | 100-2.4 | 100-3.6 | 100-4.8 | … |
(1)写出乘车的次数x表示余额y的关系式.
(2)利用上述关系式计算小明乘了15次车还剩下多少元?
(3)余额还有40元时,小明已使用此卡乘车多少次?
(4)小强最多能乘几次车?