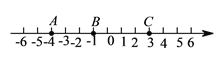题目内容
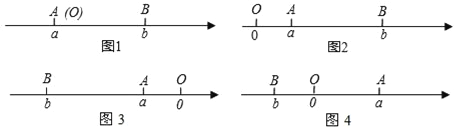
【题目】阅读下面材料：已知点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为|AB|，当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|=|OB|=|b|=|a﹣b|，当A、B两点都不在原点时．
（1）如图2，点A、B都在原点的右边，|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
（2）如图3，点A、B都在原点的左边，|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣（﹣a）=a﹣b=|a﹣b|
（3）如图4，点A、B在原点的两边，|AB|=|OA|+|OB|=|a|+|b|=a+（﹣b）=a﹣b=|a﹣b|
综上，数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题：
（1）数轴上表示2和5的两点之间的距离是 ，数轴上表示﹣2和﹣5的两点之间的距离是 ，数轴上表示﹣2和5的两点之间的距离是 ；
（2）数轴上表示x和﹣1的两点A和B之间的距离是 ，如果|AB|=2那么x为 ．
（3）若x表示一个有理数，则|x﹣1|+|x+3|有最小值吗？若有，请求出最小值；若没有，请说明理由．
【答案】（1）3；3；7；（2）|x+1|，1或﹣3；（3）4.
【解析】试题分析：（1）数轴上表示2和5的两点之间的距离是|5－2|=3，－2和－5的两点之间的距离是|－2－（－5）|=3，表示－2和5的两点之间的距离是|5－（－2）|=7；（2）数轴上表示x和－1的两点A和B之间的距离是|x－（－1）|=|x+1|，令|x+1|=2，解得x=1或－3；（3）代数式|x－1|+|x+3|表示数轴上一点到1、－3两点的距离的和，根据两点之间线段最短可知，有最小值为：1－（－3）=4．
试题解析：
（1）数轴上表示2和5的两点之间的距离是：|5－2|=3，
数轴上表示－2和－5的两点之间的距离是|－2－（－5）|=3，
数轴上表示－2和5的两点之间的距离是|5－（－2）|=7；
（2）数轴上表示x和－1的两点之间的距离是|x+1|，|AB|=2，则|x+1|=2，故x=1或－3；
（3）代数式|x－1|+|x+3|表示数轴上一点到1、－3两点的距离的和，根据两点之间线段最短可知，有最小值为：1－（－3）=4．
