题目内容
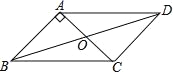
【题目】如图,在![]() 中,
中,![]() 分别平分
分别平分![]() 和
和![]() ,交
,交![]() 于点
于点![]() ,线段
,线段![]() 相交于点M.
相交于点M.
(1)求证:![]() ;
;
(2)若![]() ,则
,则![]() 的值是__________.
的值是__________.

【答案】(1)略;(2)![]() ;
;
【解析】
(1)想办法证明∠BAE+∠ABF=90°,即可推出∠AMB=90°即AE⊥BF;
(2)证明DE=AD,CF=BC,再利用平行四边形的性质AD=BC,证出DE=CF,得出DF=CE,由已知得出BC=AD=5EF,DE=5EF,求出DF=CE=4EF,得出AB=CD=9EF,即可得出结果.
(1)证明:∵在平行四边形ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°,
∵AE、BF分别平分∠DAB和∠ABC,
∴∠DAB=2∠BAE,∠ABC=2∠ABF,
∴2∠BAE+2∠ABF=180°,即∠BAE+∠ABF=90°,
∴∠AMB=90°,
∴AE⊥BF;
(2)解:∵在平行四边形ABCD中,CD∥AB,
∴∠DEA=∠EAB,
又∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DEA=∠DAE,
∴DE=AD,同理可得,CF=BC,
又∵在平行四边形ABCD中,AD=BC,
∴DE=CF,
∴DF=CE,
∵EF=![]() AD,
AD,
∴BC=AD=5EF,
∴DE=5EF,
∴DF=CE=4EF,
∴AB=CD=9EF,
∴BC:AB=5:9;
故答案为:5:9.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
【题目】某校七(1)班学生的平均身高是160厘米,下表给出了该班6名学生的身高情况(单位:厘米).
学 生 | A | B | C | D | E | F |
身 高 | 157 | 162 | 159 | 154 | 163 | 165 |
身高与平均身高的差值 | -3 | +2 | -1 | a | +3 | b |
(1)列式计算表中的数据a和b;
(2)这6名学生中谁最高?谁最矮?最高与最矮学生的身高相差多少?
(3)这6名学生的平均身高与全班学生的平均身高相比,在数值上有什么关系?(通过计算回答)