题目内容
【题目】某高中进行“选科走班”教学改革，语文、数学、英语三门为必修学科，另外还需从物理、化学、生物、政治、历史、地理（分别记为A、B、C、D、E、F）六门选修学科中任选三门，现对该校某班选科情况进行调查，对调查结果进行了分析统计，并制作了两幅不完整的统计图．
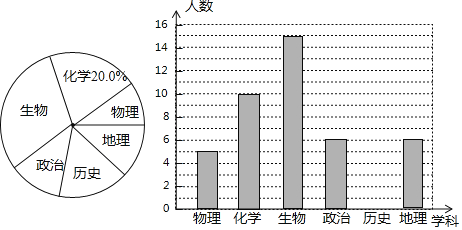
请根据以上信息，完成下列问题：
（1）该班共有学生人；
（2）请将条形统计图补充完整；
（3）该班某同学物理成绩特别优异，已经从选修学科中选定物理，还需从余下选修学科中任意选择两门，请用列表或画树状图的方法，求出该同学恰好选中化学、历史两科的概率．
【答案】（1）50人；（2）补图见解析；（3）
.
【解析】（1）根据化学学科人数及其所占百分比可得总人数；
（2）根据各学科人数之和等于总人数求得历史的人数即可；
（3）列表得出所有等可能结果，从中找到恰好选中化学、历史两科的结果数，再利用概率公式计算可得．
（1）该班学生总数为10÷20%=50人；
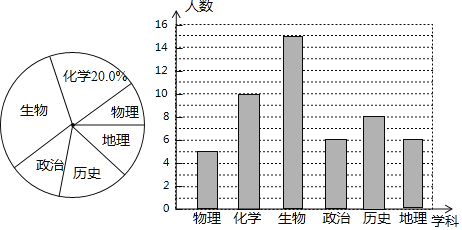
（2）历史学科的人数为50﹣（5+10+15+6+6）=8人，
补全图形如下：
（3）列表如下：
化学 | 生物 | 政治 | 历史 | 地理 | |
化学 | 生物、化学 | 政治、化学 | 历史、化学 | 地理、化学 | |
生物 | 化学、生物 | 政治、生物 | 历史、生物 | 地理、生物 | |
政治 | 化学、政治 | 生物、政治 | 历史、政治 | 地理、政治 | |
历史 | 化学、历史 | 生物、历史 | 政治、历史 | 地理、历史 | |
地理 | 化学、地理 | 生物、地理 | 政治、地理 | 历史、地理 |
由表可知，共有20种等可能结果，其中该同学恰好选中化学、历史两科的有2种结果，
所以该同学恰好选中化学、历史两科的概率为
．
【题目】为了满足学生的物质需求，我市某中学到红旗超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表：
甲 | 乙 | |
进价（元/袋） |
|
|
售价（元/袋） | 20 | 13 |
已知：用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
（1）求
的值；
（2）要使购进的甲、乙两种绿色袋装食品共800袋的总利润（利润=售价-进价）不少于5200元，且不超5280元，问该红旗超市有几种进货方案？
（3）在（2）的条件下，该红旗超市准备对甲种袋装食品进行优惠促销活动，决定对甲种袋装食品每袋优惠
元出售，乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货？
【题目】借助表格进行多项式乘多项式运算，可以方便合并同类项得出结果．下面尝试利用表格试一试．
例题：（a+b）（a﹣b）
解填表
| a | b |
a | a2 | ab |
﹣b | ﹣ab | ﹣b2 |
则（a+b）（a﹣b）＝a2﹣b2．
根据所学完成下列问题．
（1）如表，填表计算（x+2）（x2﹣2x+4），（m+3）（m2﹣3m+9），直接写出结果．
| x2 | ﹣2x | 4 |
x | x3 | ﹣2x2 | 4x |
+2 | 2x2 | ﹣4x | 8 |
| m2 | ﹣3m | 9 |
m | m3 | ﹣3m2 | 9m |
+3 | 3m2 | ﹣9m | 27 |
结果为 ；结果为 ．
（2）根据以上获得的经验填表：
| |||
△ | △3 | ||
〇 | 〇3 |
结果为△3+〇3，根据以上探索，请用字母a、b来表示发现的公式为 ．
（3）用公式计算：（2x+3y）（4x2﹣6xy+9y2）＝ ；
因式分解：27m3﹣8n3＝ ．
