题目内容
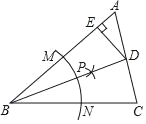
【题目】如图l,在![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() 和
和![]() 上,点
上,点![]() ,
,![]() 在对角线
在对角线![]() 上,且
上,且![]() ,
,![]() .
.
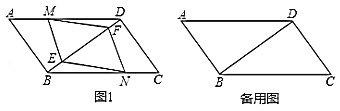
(1)求证:四边形![]() 是平行四边形:
是平行四边形:
(2)若![]() ,
,![]() ,
,![]() .
.
①当四边形![]() 是菱形时,
是菱形时,![]() 的长为______;
的长为______;
②当四边形![]() 是正方形时,
是正方形时,![]() 的长为______;
的长为______;
③当四边形![]() 是矩形且
是矩形且![]() 时,
时,![]() 的长为______.
的长为______.
【答案】(1)证明见解析,(2)①5.②1.③![]() .
.
【解析】
(1)如图1中,设![]() 的中点为
的中点为![]() .连接
.连接![]() ,
,![]() ,
,![]() ,
,![]() .利用对角线互相平分的四边形是平行四边形证明即可.
.利用对角线互相平分的四边形是平行四边形证明即可.
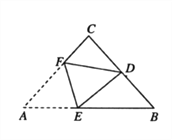
(2)①如图![]() 中,连接
中,连接![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,四边形
时,四边形![]() 是菱形.利用平行线等分线段定理即可解决问题.
是菱形.利用平行线等分线段定理即可解决问题.
②在①的基础上,![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
③如图![]() 中,连接
中,连接![]() 交
交![]() 于点
于点![]() ,作
,作![]() 于
于![]() .当
.当![]() 时,四边形
时,四边形![]() 是矩形.
是矩形.
(1)证明:如图1中,设![]() 的中点为
的中点为![]() .连接
.连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
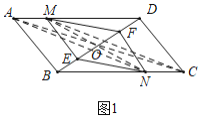
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 与
与![]() 互相平分且交于点
互相平分且交于点![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 与
与![]() 互相平分且交于点
互相平分且交于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
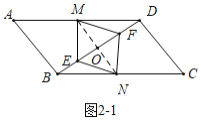
(2)①如图![]() 中,连接
中,连接![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,四边形
时,四边形![]() 是菱形.
是菱形.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
②在①的基础上,满足![]() 时,四边形
时,四边形![]() 是正方形,
是正方形,
易知![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
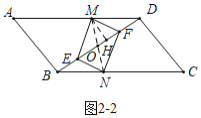
③如图![]() 中,连接
中,连接![]() 交
交![]() 于点
于点![]() ,作
,作![]() 于
于![]() .
.
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,四边形
时,四边形![]() 是矩形,
是矩形,
![]() .
.
故答案为:5,1,![]() .
.

练习册系列答案
相关题目