题目内容
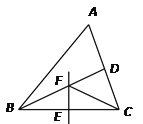
【题目】如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF.若∠A=60°,∠ACF =45°,则∠ABC的度数为( )
A. 45° B. 50° C. 55° D. 60°
【答案】B
【解析】 设∠ABD=∠CBD=x°,则∠ABC=2x°,根据线段垂直平分线性质求出BF=CF,推出∠FCB=∠CBD,根据三角形内角和定理得出方程,求出方程的解即可.
解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
设∠ABD=∠CBD=x°,则∠ABC=2x°,
∵EF是BC的垂直平分线,
∴BF=CF,
∴∠FCB=∠CBD=x°,
∵∠A=60°,∠ACF=45°,
∴60°+45°+x°+2x°=180°,
解得:x=25,
∴∠ABC=2x°=50°,
故选B.
“点睛”本题考查了三角形内角和定理,线段垂直平分线性质的应用,能求出BF=CF是解此题的关键,注意线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目