Question

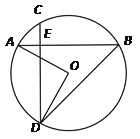
【题目】如图，在⊙O中，弦AB=弦CD，AB⊥CD于点E，且AE＜EB，CE＜ED，连结AO，DO，BD．

（1）求证：EB=ED．

（2）若AO=6，求的长．

Answer 1

【答案】（1）证明见解析；（2）的长为

【解析】（1）由AB=CD，根据圆心角、弧、弦的关系定理得出=．即+=+，那么=，根据圆周角定理得到∠CDB=∠ABD，利用等角对等边得出

EB=ED；

（2）先求出∠CDB=∠ABD=45°，再根据圆周角定理得出∠AOB=90°．又AO=6，代入弧长公式计算即可求解．

（1）证明：∵AB=CD，∴=．即+=+．

∴=．∵、所对的圆周角分别为∠CDB，∠ABD，

∴∠CDB=∠ABD．∴EB=ED．

（2）解：∵AB⊥CD，∴∠CDB=∠ABD=45°．

∵AO=6，∴的长．

“点睛”本题考查了弧长的计算，圆心角、弧、弦的关系，圆周角定理，等腰三角形判定，证明出∠CDB=∠ABD是解题的关键．