题目内容
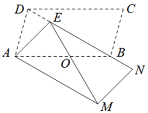
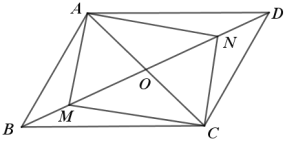
【题目】如图,已知平行四边形ABCD.
(1)若M,N是BD上两点,且BM=DN,AC=2OM,求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC,求平行四边形ABCD的面积.
【答案】(1)见解析;(2)16![]() .
.
【解析】
(1)由平行四边形的性质可知:OA=OC,OB=OD,再证明OM=ON即可证明四边形AMCN是平行四边形;
(2)根据平行四边形的性质得到AD∥BC,AB=CD=4,求得∠ABC=60°,解直角三角形即可得到结论.
(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=4,
∴∠BAD+∠ABC=180°,
∵∠BAD=120°,
∴∠ABC=60°,
∵AB⊥AC,
∴∠BAC=90°,
∴AC=![]() AB=4
AB=4![]() ,
,
∴平行四边形ABCD的面积=ACAB=4![]() 4=16
4=16![]() .
.

 轻巧夺冠周测月考直通中考系列答案
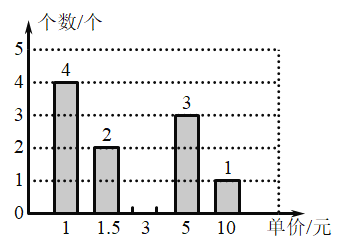
轻巧夺冠周测月考直通中考系列答案【题目】今年在2月27日国务院对外新闻发布会上,中国疾控中心发言人提到:“在新冠肺炎低风险区域出行仍需戴口罩.”某单位复工,采购了一批医用外科口罩,单价分别为1元、1.5元、3元、5元、10元,每天随机配发给每位在岗员工一个口罩.现将连续10天口罩配发量的情况制成如下统计表.
配发量/个 | 30 | 25 | 20 | 15 |
天数/天 | 2 |
|
| 1 |
已知配发量的平均数是23个,中位数是![]() 个,众数是
个,众数是![]() 个.
个.
(1)求![]() 的值,并计算
的值,并计算![]() ;
;
(2)将配发15个口罩那一天中不同型号的口罩发放情况进行统计,绘制成如图所示的尚不完整的统计图.补全统计图,并求小李当天获得不低于3元口罩的概率;
(3)若继续发放两天口罩,且这12天口罩配发量的众数与前10天口罩配发量的众数不同(例如:只要在第11天,第12天都发放30个口罩,则这12天口罩发放量的众数为30个和20个),写出这12天口罩配发量的众数(括号内示例情况不必再述).