��Ŀ����
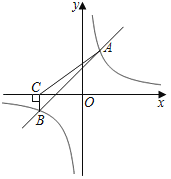
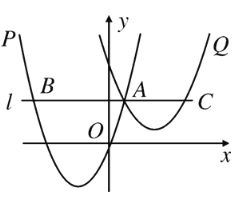
����Ŀ����ͼ��������P��y1��a��x��2��2��3��������Q��y2��![]() ��x��t��2��1��ͬһ������ϵ�У�����a��t��Ϊ��������t��0������֪������P����A��1��3��������A��ֱ��l��x�ᣬ��������P�ڵ�B��
��x��t��2��1��ͬһ������ϵ�У�����a��t��Ϊ��������t��0������֪������P����A��1��3��������A��ֱ��l��x�ᣬ��������P�ڵ�B��
��1��a��________����B��������________��
��2����������Q������Aʱ��
����������Q�Ľ���ʽ��
����ֱ��l��������Q����һ�������C����![]() ��ֵ��
��ֵ��
��3����������Q���߶�AB����Ψһ�Ľ��㣬ֱ��д��t��ȡֵ��Χ��
���𰸡���1�� ![]() ������5��3������2����������Q�Ľ���ʽΪ��y2��
������5��3������2����������Q�Ľ���ʽΪ��y2�� ![]() ��x��3��2��1����
��x��3��2��1����![]() ��
��![]() ����3��0��t
����3��0��t![]() 3��
3��
��������
��1�������ô���ϵ�������������P�Ľ���ʽ�����ɵó����ۣ�
��2�������ô���ϵ�������������Q�Ľ���ʽ�����ɵó����ۣ��������AC��AB���ɵó����ۣ�
��3������ƽ�Ƶ��ص��AB��AC�ij����ɵó����ۣ�
�⣺��1����������P��y1��a��x��2��2��3����A��1��3����
��9a��3��3��
��a��![]() ��
��
��������P��y1�� ![]() ��x��2��2��3��
��x��2��2��3��
��![]()
![]() x�ᣬ
x�ᣬ
���B��������Ϊ3��
��3�� ![]() ��x��2��2��3��
��x��2��2��3��
��x1��1����A�ĺ����꣩��x2����5��
��B����5��3����
��2���١�������Q��y2��![]() ��x��t��2��1����A��1��3����
��x��t��2��1����A��1��3����
��![]() ��1��t��2��1��3��
��1��t��2��1��3��
��t1����1����ȥ����t2��3��
��������Q�Ľ���ʽΪ��y2�� ![]() ��x��3��2��1��
��x��3��2��1��
��![]()
![]() x�ᣬ
x�ᣬ
���C��������Ϊ3��
��3��![]() ��x��3��2��1��
��x��3��2��1��
��x1��1����A�ĺ����꣩��x2��5��
��C��5��3����
��AC��5��1��4��
�ɣ�1��֪��B����5��3����
��AB��1������5����6��
��![]() ��
��![]() ��
��![]() ��
��
��3����������Q��y2��![]() ��x��t��2��1
��x��t��2��1
��������Q�Ŀ��ڴ�Сһ���������������������1Ҳ�Ƕ�ֵ��
��������Qֻ�������ƶ���
��������Q����ƽ�ƵĹ����У���A��������Q�����ʱ��������Q���߶�AB��һ������A����ʱ��t=3��
�ɣ�2��֪��AC=4����������Q����ƽ��4����λʱ�����߶�AB���������㣬�˶Σ���1��t![]() 3ʱ��������Q���߶�AB��һ�����㣬
3ʱ��������Q���߶�AB��һ�����㣬
�ټ�����������Q�����ƶ����ƶ�����B��������Q�����ʱ����ʱ����ʱ��t=��3��
ͬ�ϣ�������Q���߶�AB��һ�����㣬��7![]() t����3��
t����3��
��t��0��
����0��t![]() 3��������Q���߶�AB��һ�����㣮
3��������Q���߶�AB��һ�����㣮

 ��У����ϵ�д�
��У����ϵ�д�