题目内容
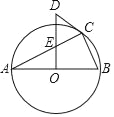
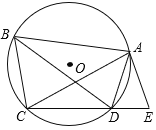
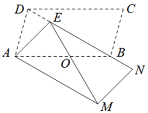
【题目】如图，平行四边形ABCD中，BD=AB，∠ABD=30°，将平行四边形ABCD绕点A旋转至平行四边形AMNE的位置，使点E落在BD上， ME交AB于点O， 则
的值是（ ）
A.
B.
C.
D.
【答案】B
【解析】
过点E作EF⊥AB于点F，根据角度关系可以求出△AEF为等腰直角三角形，设EF=x，则AF=x，可求得
，由△AOM∽△BOE，即可求出结果.
解：过点E作EF⊥AB于点F，如图：
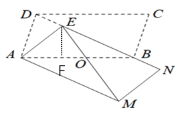
∵BD=AB，
，
∴
，
∵平行四边形ABCD绕点A旋转至平行四边形AMNE的位置，
∴AB=AM，AD=AE，
∴
,
∴
,
∴
,
∵EF⊥AB，
∴
,
∴
,
∴△AEF为等腰直角三角形，
∴EF=AF，
设EF=x，则AF=x，
在Rt△BEF中，，
∴
，
，
∵AM∥BE，
∴△AOM∽△BOE，
∴
，
故选：B.
练习册系列答案
相关题目
【题目】某班兴趣小组对函数y＝﹣x2+2|x|的图象和性质进行了探究，探究过程如下，请补充完整．
（1）自变量的取值范围是全体实数，x与y的几组对应值列表如下：
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣3 |
| 0 | 1 | 0 | 1 | 0 |
| ﹣3 | … |
（1）根据上表数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该图象的另一部分；
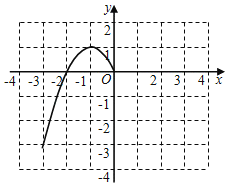
（2）观察函数图象，当y随x增大而减小时，则x的取值范围是
（3）进一步探究函数图象发现：
①函数图象与x轴有 个交点，所以对应方程﹣x2+2|x|＝0有 个实数根；
②方程﹣x2+2|x|＝﹣1有 个实数根；
③若关于x的方程﹣x2+2|x|＝n有4个实数根，则n的取值范围是 ．
