题目内容
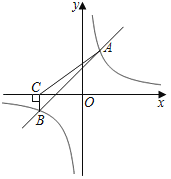
【题目】如图，点A、B为直线y＝x上的两点，过A、B两点分别作y轴的平行线交双曲线
（x＞0）于点C、D两点．若BD＝2AC，则4OC2﹣OD2的值为（ ）
A.5B.6C.7D.8
【答案】B
【解析】
延长AC交x轴于E，延长BD交x轴于F，设A、B的横坐标分别是a，b，得到C（a，
），D（b，
），根据BD=2AC求出b-=2（a-），两边同时平方整理得
，利用勾股定理证得OC2=OE2+CE2=
，OD2=
，由此即可求出答案.
延长AC交x轴于E，延长BD交x轴于F，
设A、B的横坐标分别是a，b，
∵点A、B为直线y=x上的两点，
∴A的坐标是（a，a），B的坐标是（b，b）．则AE=OE=a，BF=OF=b，
∵过A、B两点分别作y轴的平行线交双曲线
（x＞0）于点C、D两点，
∴C（a，），D（b，），
∴AC=a-，BD=b-，
∵BD=2AC，
∴b-=2（a-），
∴
，
∴，
在直角△OCE中，OC2=OE2+CE2=，
同理OD2=，
∴4OC2﹣OD2=4（）-（）=6，
故选：B
练习册系列答案
名校课堂系列答案
相关题目
