ÌâÄżÄÚÈĘ
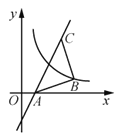
ĄŸÌâÄżĄżÄłč«ËŸŃĐ·ąÁËÒ»żîĐÂĐÍÍæŸßŁŹłÉ±ŸÎȘĂżžö50ÔȘŁŹÍ¶·ĆÊĐłĄœűĐĐÊÔÏúÊÛŁźÆäÏúÊÛ”„ŒÛČ»”ÍÓڳɱŸŁŹ°ŽŐŐÎïŒÛČżĂĆč涚ŁŹÏúÊÛÀûÈóÂÊČ»žßÓÚ70%ŁŹÊĐłĄ”śŃĐ·ąÏÖŁŹÔÚÒ»¶ÎʱŒäÄÚŁŹĂżÌìÏúÊÛÊęÁżyŁšžöŁ©ÓëÏúÊÛ”„ŒÛxŁšÔȘŁ©ŁšxÎȘŐûÊ꣩·ûșÏÒ»ŽÎșŻÊęčŰÏ”ŁŹÈçÍŒËùÊŸ
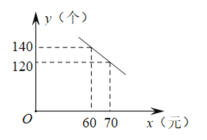
Łš1Ł©ÇółöyÓëx”ÄșŻÊęčŰϔʜŁŹČąĐŽłöŚÔ±äÁżx”ÄÈĄÖ”·¶Î§Ł»
Łš2Ł©žĂč«ËŸÒȘÏëĂżÌì»ń”Ă3000ÔȘ”ÄÏúÊÛÀûÈóŁŹÏúÊÛ”„ŒÛÓŠ¶šÎȘ¶àÉÙÔȘŁż
Łš3Ł©ÏúÊÛ”„ŒÛÎȘ¶àÉÙÔȘʱŁŹĂżÌì»ń”Ă”ÄÀûÈóŚîŽóŁŹŚîŽóÀûÈóÊǶàÉÙÔȘŁż
ĄŸŽđ°žĄżŁš1Ł©y=-2x+260Łš![]() Ł©Ł»Łš2Ł©80ÔȘŁ»Łš3Ł©ÏúÊÛ”„ŒÛÎȘ85ÔȘʱŁŹĂżÌì»ń”Ă”ÄÀûÈóŚîŽóŁŹŚîŽóÀûÈóÊÇ3150ÔȘ
Ł©Ł»Łš2Ł©80ÔȘŁ»Łš3Ł©ÏúÊÛ”„ŒÛÎȘ85ÔȘʱŁŹĂżÌì»ń”Ă”ÄÀûÈóŚîŽóŁŹŚîŽóÀûÈóÊÇ3150ÔȘ
ĄŸœâÎöĄż
Łš1Ł©ÓÉŽę¶šÏ”Êę·šżÉ”ĂșŻÊę”ÄœâÎöÊœŁ»
Łš2Ł©žùŸĘÀûÈó”ÈÓÚĂżŒț”ÄÀûÈółËÒÔÏúÊÛÁżŁŹÁĐ·œłÌżÉœâŁ»
Łš3Ł©ÉèĂżÌì»ń”Ă”ÄÀûÈóÎȘwÔȘŁŹÓÉÌâÒâ”öțŽÎșŻÊ꣏ЎłÉ¶„”ăÊœŁŹżÉÇó”Î𰞣ź
œâŁșŁš1Ł©Éèy=kx+bŁškĄÙ0ŁŹbÎȘłŁÊ꣩
œ«”㣚60ŁŹ140Ł©ŁŹŁš70ŁŹ120Ł©ŽúÈë”ĂŁș
![]() ŁŹœâ”Ă
ŁŹœâ”Ă![]() ŁŹ
ŁŹ
ĄàyÓëx”ÄșŻÊęčŰϔʜÎȘŁșy=-2x+260ŁŹ
œâČ»”ÈÊœŚé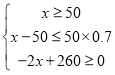 ŁŹ
ŁŹ
”ĂŁș![]() ÇÒxÎȘŐûÊꣻ
ÇÒxÎȘŐûÊꣻ
Łš2Ł©ÓÉÌâÒâ”ĂŁș![]() ŁŹ
ŁŹ
»ŻŒò”ĂŁșx2-180x+8000=0ŁŹ
œâ”ĂŁșx1=80ŁŹx2=100ŁŹ
Ąß![]() =85ŁŹ
=85ŁŹ
Ąàx2=100ŁŸ85ŁšČ»·ûșÏÌâÒ⣏ÉáÈ„Ł©
ŽđŁșÏúÊÛ”„ŒÛÎȘ80ÔȘŁ»
Łš3Ł©ÉèĂżÌì»ń”Ă”ÄÀûÈóÎȘwÔȘŁŹÓÉÌâÒâ”ĂŁŹ
![]() ŁŹ
ŁŹ
=-2x2+360x-13000
=-2(x-90)2+3200
Ąßa=-2ŁŒ0ŁŹĆŚÎïÏßżȘżÚÏòÏÂŁŹ
ĄàwÓĐŚîŽóÖ”ŁŹ
Ąß![]() ŁŹ
ŁŹ
Ąà”±x=85ʱŁŹwŚîŽóÖ”=3150ŁŹ
ŽđŁșÏúÊÛ”„ŒÛÎȘ85ÔȘʱŁŹĂżÌì»ń”Ă”ÄÀûÈóŚîŽóŁŹŚîŽóÀûÈóÊÇ3150ÔȘ.

 ÔĶÁżìł”Ï”ÁĐŽđ°ž
ÔĶÁżìł”Ï”ÁĐŽđ°ž