题目内容
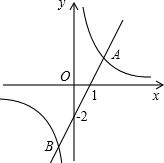
已知反比例函数y=
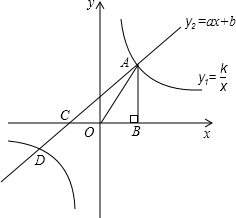
图象过第二象限内的点A(-2,m)AB⊥x轴于B,Rt△AOB面积为3.
(1)求k和m的值;
(2)若直线y=ax+b经过点A,并且经过反比例函数y=
的图象上另一点C(n,-
).
①求直线y=ax+b的关系式;
②据图象写出使反比例函数y=
的值大于一次函数y=ax+b的值的x的取值范围.
| k |
| x |
(1)求k和m的值;
(2)若直线y=ax+b经过点A,并且经过反比例函数y=
| k |
| x |
| 3 |
| 2 |
①求直线y=ax+b的关系式;
②据图象写出使反比例函数y=
| k |
| x |

(1)∵A(-2,m),即AO=2,Rt△AOB面积为3,
∴AB=3,
∴A(-2,3),m=3;
将A坐标代入反比例解析式得:k=-6;
(2)①将C(n,-
)代入反比例解析式得:n=4,即C(4,-
),
将A与C坐标代入一次函数y=ax+b中,得:
,
解得:
,
∴一次函数解析式为y=-
x+
;
②由A、C的横坐标分别为-2和4,
利用图象得:反比例函数的值大于一次函数的值的x的取值范围为-2<x<0或x>4.
∴AB=3,
∴A(-2,3),m=3;
将A坐标代入反比例解析式得:k=-6;
(2)①将C(n,-
| 3 |
| 2 |
| 3 |
| 2 |
将A与C坐标代入一次函数y=ax+b中,得:
|
解得:
|
∴一次函数解析式为y=-
| 3 |
| 4 |
| 3 |
| 2 |
②由A、C的横坐标分别为-2和4,
利用图象得:反比例函数的值大于一次函数的值的x的取值范围为-2<x<0或x>4.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
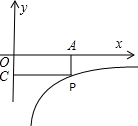

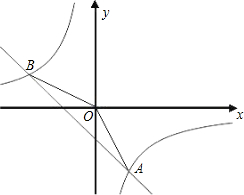 其中A点的横坐标与B点的纵坐标都是2,如图:
其中A点的横坐标与B点的纵坐标都是2,如图: