题目内容
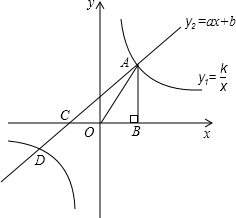
如图,已知反比例函数y=
的图象与一次函数y=k2x+b的图象交于A、B两点,A(2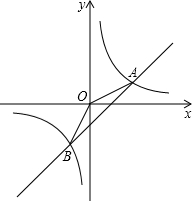 ,n),B(-1,-2).
,n),B(-1,-2).
(1)求反比例函数和一次函数的关系式;
(2)在直线AB上是否存在一点P,使△APO∽△AOB?若存在,求P点坐标;若不存在,请说明理由.
| k1 |
| x |
 ,n),B(-1,-2).
,n),B(-1,-2).(1)求反比例函数和一次函数的关系式;
(2)在直线AB上是否存在一点P,使△APO∽△AOB?若存在,求P点坐标;若不存在,请说明理由.
(1)∵双曲线y=
过点(-1,-2)
∴k1=-1×(-2)=2
∵双曲线y=
过点(2,n)
∴n=1
由直线y=k2x+b过点A,B得
,
解得
∴反比例函数关系式为y=
,一次函数关系式为y=x-1.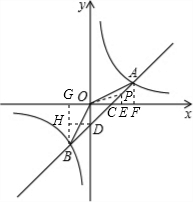
(2)存在符合条件的点P,P(
,
).
理由如下:∵A(2,1),B(-1,-2),
∴OA=
=
,AB=
=3
,
∵△APO∽△AOB
∴
=
,
∴AP=
=
=
,
如图,设直线AB与x轴、y轴分别相交于点C、D,过P点作PE⊥x轴于点E,连接OP,作AF⊥x轴,BG⊥x轴,DH⊥BG.
在直线y=x-1中,令x=0,解得:y=-1,则D的坐标是:(0,-1);
在直线y=x-1中,令y=0,解得:x=1,则C的坐标是(1,0);
则CF=OF-OC=2-1=1,AF=1,在直角△ACF中,AC=
=
,
OC=OD=1,则CD=
=
,
BH=BG-GH=2-1=1,DH=1,在直角△BDH中,BD=
=
,
则AC=CD=DB=
,
故PC=AC-AP=
-
=
,
在直线y=x-1中,令x=0,则y=-1,则D的坐标是(0,-1),OD=1,
令y=0,则x=1,则C的坐标是:(1,0),则OC=1,
则△OCD是等腰直角三角形.
∴∠OCD=45°,
∴∠ACE=∠OCD=45°.
再由∠ACE=45°得CE=PE=
×
=
,
从而OE=OC+CE=
,
点P的坐标为P(
,
).
| k1 |
| x |
∴k1=-1×(-2)=2
∵双曲线y=
| 2 |
| x |
∴n=1
由直线y=k2x+b过点A,B得
|
解得
|
∴反比例函数关系式为y=
| 2 |
| x |

(2)存在符合条件的点P,P(
| 7 |
| 6 |
| 1 |
| 6 |
理由如下:∵A(2,1),B(-1,-2),
∴OA=
| 22+12 |
| 5 |
| (-1-2)2+(-2-1)2 |
| 2 |
∵△APO∽△AOB
∴
| AP |
| AO |
| AO |
| AB |
∴AP=
| AO2 |
| AB |
| 5 | ||
3
|
5
| ||
| 6 |
如图,设直线AB与x轴、y轴分别相交于点C、D,过P点作PE⊥x轴于点E,连接OP,作AF⊥x轴,BG⊥x轴,DH⊥BG.
在直线y=x-1中,令x=0,解得:y=-1,则D的坐标是:(0,-1);
在直线y=x-1中,令y=0,解得:x=1,则C的坐标是(1,0);
则CF=OF-OC=2-1=1,AF=1,在直角△ACF中,AC=
| AF2+CF2 |
| 2 |
OC=OD=1,则CD=
| OC2+OD2 |
| 2 |
BH=BG-GH=2-1=1,DH=1,在直角△BDH中,BD=
| BH2+DH2 |
| 2 |
则AC=CD=DB=
| 2 |
故PC=AC-AP=
| 2 |
5
| ||
| 6 |
| ||
| 6 |
在直线y=x-1中,令x=0,则y=-1,则D的坐标是(0,-1),OD=1,
令y=0,则x=1,则C的坐标是:(1,0),则OC=1,
则△OCD是等腰直角三角形.
∴∠OCD=45°,
∴∠ACE=∠OCD=45°.
再由∠ACE=45°得CE=PE=
| ||
| 6 |
| ||
| 2 |
| 1 |
| 6 |
从而OE=OC+CE=
| 7 |
| 6 |
点P的坐标为P(
| 7 |
| 6 |
| 1 |
| 6 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目