题目内容
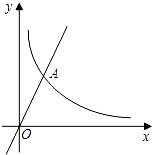
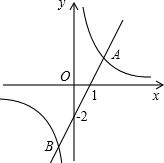
如图，在第一象限内，点P（2，3），M（a，2）是双曲线y=
（k≠0）上的两点，PA⊥x轴于点A，MB⊥x轴于点B，PA与OM交于点C，则△OAC的面积为（ ）
| k |
| x |
A．
| B．
| C．2 | D．
|
把P（2，3），M（a，2）代入y=
得k=2×3=2a，解得k=6，a=3，
设直线OM的解析式为y=mx，
把M（3，2）代入得3m=2，解得m=
，
所以直线OM的解析式为y=
x，当x=2时，y=
×2=
，
所以C点坐标为（2，
），
所以△OAC的面积=
×2×
=
．
故选B．
| k |
| x |
设直线OM的解析式为y=mx，
把M（3，2）代入得3m=2，解得m=
| 2 |
| 3 |
所以直线OM的解析式为y=
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
所以C点坐标为（2，
| 4 |
| 3 |
所以△OAC的面积=
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
故选B．
练习册系列答案
应用题作业本系列答案
相关题目
