ЬтФПФкШн
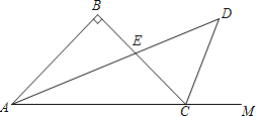
ЁОЬтФПЁПдкОиаЮABCDжаЃЌGЮЊADЩЯвЛЕуЃЌСЌНгBGЃЌCGЃЌзїCEЁЭBGгкЕуEЃЌСЌНгEDНЛGCгкЕуFЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌШєЕуGЮЊADЕФжаЕуЃЌдђЯпЖЮBGгыCGгаКЮЪ§СПЙиЯЕЃПЧыЫЕРэгЩЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌШєЕуEЧЁКУЮЊBGЕФжаЕуЃЌЧвAB=3ЃЌAG=kЃЈ0ЃМkЃМ3ЃЉЃЌЧѓ![]() ЕФжЕЃЈгУКЌkЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЕФжЕЃЈгУКЌkЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉгаЬѕМўЯТЃЌШєMЁЂNЗжБ№ЮЊGCЁЂECЩЯЕФШЮвтСНЕуЃЌСЌНгNFЁЂNMЃЌЕБk=![]() ЪБЃЌЧѓNF+NMЕФзюаЁжЕЃЎ
ЪБЃЌЧѓNF+NMЕФзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉGB=GCЃЎРэгЩМћНтЮіЃЛЃЈ2ЃЉ![]() =
=![]() ЃЛЃЈ3ЃЉNF+NMЕФзюаЁжЕЪЧ
ЃЛЃЈ3ЃЉNF+NMЕФзюаЁжЕЪЧ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
1ЃЉНсТлЃКGB=GCЃЎжЄУїЁїBAGЁеЁїCDGМДПЩЃЛ
ЃЈ2ЃЉИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУЕН![]() ЃЌЕУЕНBC=
ЃЌЕУЕНBC=![]() ЃЌЙ§GзїGHЁЭGDНЛDEгкHЃЌЭЦГіGЃЌEЃЎCЃЌDЫФЕуЙВдВЃЌИљОндВжмНЧЖЈРэЕУЕНЁЯGDH=ЁЯGCE=ЁЯBCE=ЁЯABGЃЌИљОнЯрЫЦШ§НЧаЮЕУ
ЃЌЙ§GзїGHЁЭGDНЛDEгкHЃЌЭЦГіGЃЌEЃЎCЃЌDЫФЕуЙВдВЃЌИљОндВжмНЧЖЈРэЕУЕНЁЯGDH=ЁЯGCE=ЁЯBCE=ЁЯABGЃЌИљОнЯрЫЦШ§НЧаЮЕУ![]() ЃЌМДПЩЕУЕННсТлЃЛ
ЃЌМДПЩЕУЕННсТлЃЛ
ЃЈ3ЃЉАбk=![]() ДњШы
ДњШы![]() ЃЌЙ§FзїFJЁЭBCгкJНЛCEгкNЃЌЗДЯђбгГЄНЛADгкHЃЌдђFHЁЭADЃЌЙ§NзїNMЁЭPCгкMЃЌдђNF+NMЕФзюаЁжЕМДЮЊFJЕФГЄЃЌМДПЩЕУЕННсТлЃЎ
ЃЌЙ§FзїFJЁЭBCгкJНЛCEгкNЃЌЗДЯђбгГЄНЛADгкHЃЌдђFHЁЭADЃЌЙ§NзїNMЁЭPCгкMЃЌдђNF+NMЕФзюаЁжЕМДЮЊFJЕФГЄЃЌМДПЩЕУЕННсТлЃЎ
ЃЈ1ЃЉНсТлЃКGB=GCЃЎ
РэгЩЃКЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁпAB=DCЃЌЁЯA=ЁЯCDG=90ЁуЃЌ
ЁпGA=GDЃЌ
ЁрЁїBAGЁеЁїCDGЃЈSASЃЉЃЌ
ЁрBG=CGЃЎ
ЃЈ2ЃЉНтЃКдкОиаЮABCDжаЃЌ
ЁпЁЯA=ЁЯABC=90ЁуЃЌ
ЁпCEЁЭBGЃЌ
ЁрЁЯCEB=90ЁуЃЌ
ЁрЁЯA=ЁЯCEBЃЌ
ЁрЁЯAGB+ЁЯABG=ЁЯABG+ЁЯGBC=90ЁуЃЌ
ЁрЁЯAGB=ЁЯGBCЃЌ
ЁрЁїABGЁзЁїECBЃЛ
Ёр![]() =
=![]() ЃЌ
ЃЌ
ЁпBG=![]() ЃЌEЮЊBGЕФжаЕуЃЌ
ЃЌEЮЊBGЕФжаЕуЃЌ
ЁрBE=![]() ЃЌ
ЃЌ
ЁрBC=![]() ЃЌ
ЃЌ
ШчЭМ1ЃЌЙ§GзїGHЁЭGDНЛDEгкH

ЁрGD=BC-AG=![]() ЃЌ
ЃЌ
ЁпЁЯBEC=ЁЯADC=90ЁуЃЌ
ЁрGЃЌEЃЎCЃЌDЫФЕуЙВдВЃЌ
ЁрЁЯGDH=ЁЯGCE=ЁЯBCE=ЁЯABGЃЌ
ЁрЁїAGBЁзЁїGHDЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
ЁрGH=![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() =
=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБk=![]() ЪБЃЌ
ЪБЃЌ![]() =
=![]() ЃЌ
ЃЌ
ШчЭМ2ЃЌЙ§FзїFJЁЭBCгкJНЛCEгкNЃЌЗДЯђбгГЄНЛADгкHЃЌ
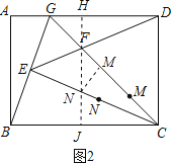
дђFHЁЭADЃЌЙ§NзїNMЁЭPCгкMЃЌ
ЁрNF+NMЕФзюаЁжЕМДЮЊFJЕФГЄЃЌ
Ёр![]() =
=![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() ЃЌЁпHJ=CD=AB=3ЃЌ
ЃЌЁпHJ=CD=AB=3ЃЌ
ЁрFJ=![]() ЃЌ
ЃЌ
МДNF+NMЕФзюаЁжЕЪЧ![]() ЃЎ
ЃЎ