题目内容
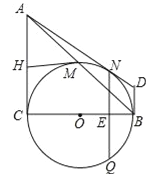
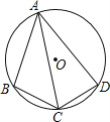
【题目】 如图,在圆O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是( )
A.4B.2![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
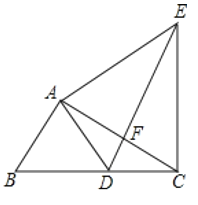
将△ACD绕点C逆时针旋转120°得△CBE,根据旋转的性质得出∠E=∠CAD=30°,BE=AD=5,AC=CE,求出A、B、E三点共线,解直角三角形求出即可.
∵A、B、C、D四点共圆,∠BAD=60°,
∴∠BCD=180°-60°=120°,
∵∠BAD=60°,AC平分∠BAD,
∴∠CAD=∠CAB=30°,
如图1,将△ACD绕点C逆时针旋转120°得△CBE,
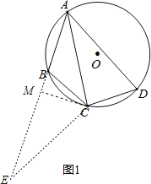
则∠E=∠CAD=30°,BE=AD=5,AC=CE,
∴∠ABC+∠EBC=(180°-∠CAB+∠ACB)+(180°-∠E-∠BCE)=180°,
∴A、B、E三点共线,
过C作CM⊥AE于M,
∵AC=CE,
∴AM=EM=![]() ×(5+3)=4,
×(5+3)=4,
在Rt△AMC中,AC=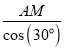 =
=![]() =
=![]() ;
;
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目