Question

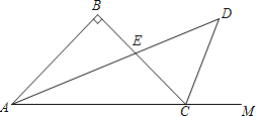
【题目】如图，在△ABC中，∠B=90°，AB=BC，∠BCM是△ABC的外角，∠BAC、∠BCM的平分线交于点D，AD与BC交于点E，若BE=2，则AEDE=____．

Answer 1

【答案】8+8．

【解析】

作EF⊥AC于F，由角平分线的性质得出FE=BE=2，证出△CEF是等腰直角三角形，再根据勾股定理表示出AE，证出DE=DC，∠CDE=45°，作EM⊥CD于M，则∠MED=45°，作∠ECN=∠CEM=22.5°，则CN=EN，∠CNM=45°，则△MDE和△MCN是等腰直角三角形，得出ME=MD，MC=MN，设MC=MN=x，在Rt△MCE中，由勾股定理得出方程，解出x，即可得到答案.

作EF⊥AC于F，如图所示：

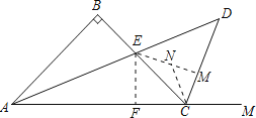
∵AD是∠BAC的平分线，∠B=90°，EF⊥AC于F，

∴FE=BE=2，

∵AB=BC，

∴∠BAC=∠ACB=45°，

∴∠BCM=135°，△CEF是等腰直角三角形，

∴FC=FE=2，CE=FE=2，

∴AB=BC=BE+CE=2+2，

∴AE===2，

∵∠BAC、∠BCM的平分线交于点D，

∴∠CAE=∠BAC=22.5°，∠DCE=∠BCM=67.5°，

∵∠DEC=∠CAE+∠ACB=67.5°=∠DCE，

∴DE=DC，∠CDE=45°，

作EM⊥CD于M，则∠MED=45°，

∴∠CEM=67.5°-45°=22.5°，

作∠ECN=∠CEM=22.5°，

则CN=EN，∠CNM=45°，

则△MDE和△MCN是等腰直角三角形，

∴ME=MD，MC=MN，

设MC=MN=x，则EN=CN=x，

∴MD=ME=x+x，

在Rt△MCE中，由勾股定理得：x2+（x+x）2=（2）2，

解得：x=，

∴DE=DC=（2+）x=（2+），

∴AEDE=2（2+）=2（2+）=8+8；

故答案为：8+8．