题目内容
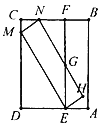
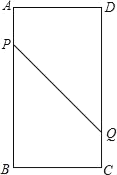
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动(不与点A,B重合);同时点Q从点C出发沿CD以2cm/s的速度向点D移动(不与点C、D重合),经过几秒,△PDQ为直角三角形?说明理由.
【答案】经过2s或![]() s或
s或![]() s时,△DPQ为直角三角形,理由见解析
s时,△DPQ为直角三角形,理由见解析
【解析】
根据题意分当∠DPQ=90°时或当∠DQP=90°时两种情况进一步分析讨论即可.
解:经过2s或![]() s或
s或![]() s时,△DPQ为直角三角形,理由如下:
s时,△DPQ为直角三角形,理由如下:
∵点P不与点A重合,
∴∠PDQ≠90°,
∴△DPQ为直角三角形分两种情况,设运动时间为x秒,
当∠DPQ=90°时,△DPQ为直角三角形,
过点Q作QM⊥AB于M,如图所示:

则四边形BCQM为矩形,
∴AP=3xcm,BM=CQ=2xcm,则PM=(16﹣5x)cm,DQ=(16﹣2x)cm,
∴(16﹣5x)2+62+(3x)2+62=(16﹣2x)2,
解得:x1=2,x2=![]() ;
;
②当∠DQP=90°时,AP+CQ=16,
所以3x+2x=16,
解得:x=![]() ,
,
综上可知:经过2s或![]() s或
s或![]() s时,△DPQ为直角三角形.
s时,△DPQ为直角三角形.

练习册系列答案
相关题目