Question

【题目】某年5月，我国南方某省A、B两市遭受严重洪涝灾害，1.5万人被迫转移，邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后，决定调运物资支援灾区. 已知C市有救灾物资240吨，D市有救灾物资260吨，现将这些救灾物资全部调往A、B两市. 已知从C市运往A、B两市的费用分别为每吨20元和25元，从D市运往往A、B两市的费用分别为每吨15元和30元，设从C市运往B市的救灾物资为x吨.

(1)请填写下表；

(2)设C、D两市的总运费为W元，求W与x之间的函数关系式，并写出自变量x的取值范围；

(3)经过抢修，从C市到B市的路况得到了改善，缩短了运输时间，运费每吨减少n元（n>0），其余路线运费不变，若C、D两市的总运费的最小值不小于10080元，求n的取值范围.

Answer 1

【答案】（1）如表见解析；（2）W=-10x+13200,; （3）

【解析】

（1）根据题意可以将表格中的空缺数据补充完整；

（2）根据题意可以求得w与x的函数关系式，并写出x的取值范围；

（3）根据题意，利用分类讨论的数学思想可以解答本题．

（1）∵C市运往B市x吨，

∴C市运往A市（240-x）吨，D市运往B市（300-x）吨，D市运往A市260-（300-x）=（x-40）吨，

故答案为：240-x、x-40、300-x；

（2）由题意可得，

w=20（240-x）+25x+15（x-40）+30(300-x)=-10x+13200，

又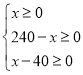得40≤x≤240,

∴w=10x+13200（40≤x≤240）；

（3）由题意可得，

w=20（240-x）+(25-n)x+15（x-40）+30(300-x)=-(n+10)x+13200，

∵n>0，

∴-(n+10)<0，

∴W随x的增大而减小

当x取最大值240时，W最小值=-(n+10)×240+13200≥10080,

即：-(n+10)×240+13200≥10080

解得，n≤3，

由上可得，m的取值范围是0＜n≤3．