Question

【题目】阅读下列材料并解决有关问题：我们知道|x|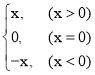＝，现在我们可以用这个结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x﹣2|时，可令x+1＝0和x﹣2＝0，分别求得x＝﹣1，x＝2（称﹣1，2分别叫做|x+1|与|x﹣2|的零点值．）在有理数范围内，零点值x＝﹣1和x＝2可将全体有理数分成不重复且不遗漏的如下3种情况：

（1）当x＜﹣1时，原式＝﹣（x+1）﹣（x﹣2）＝﹣2x+1；

（2）当﹣1≤x≤2时，原式＝x+1﹣（x﹣2）＝3；

（3）当x＞2时，原式＝x+1+x﹣2＝2x﹣1．

综上所述，原式＝．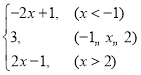

通过以上阅读，请你解决以下问题：

（1）分别求出|x+2|和|x﹣4|的零点值；

（2）化简代数式|x+2|+|x﹣4|；

（3）求方程：|x+2|+|x﹣4|＝6的整数解；

（4）|x+2|+|x﹣4|是否有最小值？如果有，请直接写出最小值；如果没有，请说明理由．

Answer 1

【答案】（1）﹣2，4分别为|x+2|和|x﹣4|的零点值；（2）当x＜﹣2时，﹣2x+2；当﹣2≤x＜4时， 6；当x≥4时， 2x﹣2；（3）整数解为：﹣2，﹣1，0，1，2，3，4；（4）有，|x+2|+|x﹣4|的最小值是6．

【解析】

（1）根据题中所给材料，求出零点值；

（2）将全体实数分成不重复且不遗漏的三种情况解答；

（3）由|x+2|+|x-4|=6，得到-2≤x≤4，于是得到结果；

（4）|x+2|+|x-4|有最小值，通过x的取值范围即可得到结果．

（1）∵|x+2|和|x﹣4|的零点值，可令x+2＝0和x﹣4＝0，解得x＝﹣2和x＝4，

∴﹣2，4分别为|x+2|和|x﹣4|的零点值．

（2）当x＜﹣2时，|x+2|+|x﹣4|＝﹣2x+2；

当﹣2≤x＜4时，|x+2|+|x﹣4|＝6；

当x≥4时，|x+2|+|x﹣4|＝2x﹣2；

（3）∵|x+2|+|x﹣4|＝6，

∴﹣2≤x≤4，

∴整数解为：﹣2，﹣1，0，1，2，3，4．

（4）|x+2|+|x﹣4|有最小值，

∵当x＝﹣2时，|x+2|+|x﹣4|＝6，

当x＝4时，|x+2|+|x﹣4|＝6，

∴|x+2|+|x﹣4|的最小值是6．