题目内容
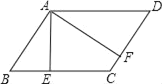
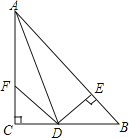
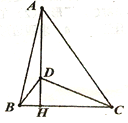
【题目】如图在△ABC中,AH⊥BC于点H,在AH上取一点D,连接DC,使DA=DC,且∠ADC=2∠DBC,若DH=2,BC=6,则AB=_________________。
【答案】![]()
【解析】
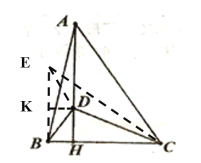
如图,过点B作BE∥DH,并在BE上取BE=2DH,连接ED,EC.并取BE的中点K,连接DK,根据垂直的定义得到∠DHC=90°,由平行线的性质得到∠EBC=90°.由线段垂直平分线的性质得到BK=DH.推出四边形DKBH为矩形,得到DK⊥BE,根据等腰三角形的性质得到DE=DB,∠EDB=2∠KDB,通过△EDC≌△BDA,得到AB=CE,根据勾股定理得到![]() ,于是得到结论.
,于是得到结论.
解:如图,过点B作BE∥DH,并在BE上取BE=2DH,连接ED,EC.并取BE的中点K,连接DK,
∵DH⊥BC于H,
∴∠DHC=90°,
∵BE∥DH,
∴∠EBC=90°,
∵∠EBC=90°,
∵K为BE的中点,BE=2DH,
∴BK=DH.
∵BK∥DH,
∴四边形DKBH为矩形,DK∥BH,
∴DK⊥BE,∠KDB=∠DBC,
∴DE=DB,∠EDB=2∠KDB,
∵∠ADC=2∠DBC,
∴∠EDB=∠ADC,
∴∠EDB+∠EDA=∠ADC+∠EDA,即∠EDC=∠BDA,
在△EDC、△BDA中,
 ,
,
∴△EDC≌△BDA,
∴AB=CE,
∴![]() ,
,
∴AB=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目