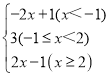题目内容
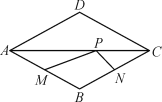
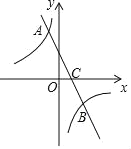
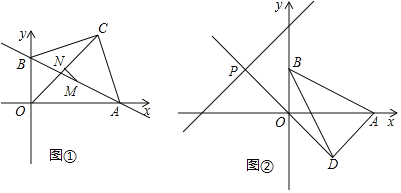
【题目】如图1,在平面直角坐标系中,直线![]() 与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
(1)直接写出![]() = ;
= ;
(2)请你过点C作CE⊥y轴于E点,试探究OB+OA与CE的数量关系,并证明你的结论;
(3)若点M为AB的中点,点N为OC的中点,求MN的值;
(4)如图2,将线段AB绕点B沿顺时针方向旋转至BD,且OD⊥AD,延长DO交直线![]() 于点P,求点P的坐标.
于点P,求点P的坐标.
【答案】(1) 4;(2)OB+OA=2CE;见解析;(3)MN=![]() ;(4)P(
;(4)P(![]() ,
,![]() ).
).
【解析】
(1)令x=0,求出y的值,令y=0,求出x的值,即可得出OA,OB的长,根据三角形面积公式即可求出结果;
(2)过点C作CF⊥x轴,垂足为点F,易证△CEB≌△CFA与四边形CEOF是正方形,从而得AF=BE,CE=BE=OF,由OB=OE-BE,AO=OF+AF可得结论;
(3)求出C点坐标,利用中点坐标公式求出点M,N的坐标,进而用两点间的距离公式求解即可得出结论;
(4)先判断出点B是AQ的中点,进而求出Q的坐标,即可求出DP的解析式,联立成方程组求解即可得出结论.
(1)∵直线y=-![]() x+2交坐标轴于A,B两点,
x+2交坐标轴于A,B两点,
令x=0,则y=2,令y=0,则x=4,
∴BO=2,AO=4,
∴![]() =
=![]() ;
;
(2)作CF⊥x轴于F,作CE⊥y轴于E,如图,
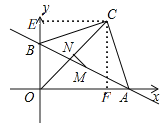
∴∠BFC=∠AEC=90°
∵∠EOF=90°,
∴四边形OECF是矩形,
∴CF=OE,CE=OF,∠ECF=90°,
∵∠ACB=90°
∴∠BCF=∠ACE,
∵BC=AC,
∴△CFB≌△CEA,
∴CF=CE,AF=BE,
∴四边形OECF是正方形,
∴OE=OF=CE=CF,
∴OB=OE-BE,OA=OF+AF,
∴OB+OA=OE+OF=2CE;
(3)由(2)得CE=3,
∴OE=3,
∴OF=3,
∴C(3,3);
∵M是线段AB的中点,而A(4,0),B(0,2),
∴M(2,1),
同理:N(![]() ,
,![]() ),
),
∴MN=![]() ;
;
(3)如图②延长AB,DP相交于Q,
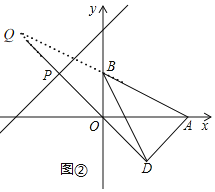
由旋转知,BD=AB,
∴∠BAD=∠BDA,
∵AD⊥DP,
∴∠ADP=90°,
∴∠BDA+∠BDQ=90°,∠BAD+∠AQD=90°,
∴∠AQD=∠BDQ,∴BD=BQ,
∴BQ=AB,
∴点B是AQ的中点,
∵A(4,0),B(0,2),
∴Q(-4,4),
∴直线DP的解析式为y=-x①,
∵直线DO交直线y=x+5②于P点,
联立①②解得,x=-![]() ,y=
,y=![]() ,
,
∴P(-![]() ,
,![]() ).
).

【题目】甲、乙两人参加射箭比赛,两人各射了5箭,他们的成绩(单位:环)统计如下表.
第1箭 | 第2箭 | 第3箭 | 第4箭 | 第5箭 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 6 | 5 | 7 |
(1)分别计算甲、乙两人射箭比赛的平均成绩;
(2)你认为哪个人的射箭成绩比较稳定?为什么?