题目内容
【题目】已知:关于x的函数y=kx2+k2x﹣2的图象与y轴交于点C,
(1)当k=﹣2时,求图象与x轴的公共点个数;
(2)若图象与x轴有一个交点为A,当△AOC是等腰三角形时,求k的值.
(3)若x≥1时函数y随着x的增大而减小,求k的取值范围.
【答案】(1)图象与x轴公共点只有一个;(2)k的值为﹣1+![]() 或﹣1﹣
或﹣1﹣![]() 或1;(3)﹣2≤k<0.
或1;(3)﹣2≤k<0.
【解析】分析:(1)△=b2-4ac=0时,抛物线与x轴有1个交点(或者把k=-2代入函数关系,直接求得抛物线与x轴的交点横坐标);
(2)根据△AOC是等腰直角三角形易求点A的坐标为(2,0)或(-2,0).把点A的坐标代入函数解析式,通过方程来求k的值;
(3)由“k≥1时函数y随着x的增大而减小”可知,抛物线开口向下.则k<0,且对称轴在直线x=1的左侧,故﹣![]() ≤1,即
≤1,即![]() ≤1.
≤1.
详解:(1)方法一:当k=﹣2时,函数为y=﹣2x2+4x﹣2,
∵b2﹣4ac=42﹣4×(﹣2)×(﹣2)=0.
∴图象与x轴公共点只有一个.
方法二:当k=﹣2时,函数为y=﹣2x2+4x﹣2,
令y=0,则﹣2x2+4x﹣2=0,
解得:x1=x2=1,
∴图象与x轴公共点只有一个;
(2)当△AOC是等腰三角形时,
∵∠AOC=90°,OC=2,
∴可得OA=OC=2.
∴点A的坐标为(2,0)或(﹣2,0).
把x=2,y=0代入解析式 得2k2+4k﹣2=0,
解得 k1=﹣1+![]() ,k1=﹣1﹣
,k1=﹣1﹣![]() ,
,
把x=﹣2,y=0代入解析式 得﹣2k2+4k﹣2=0,
解得 k1=k2=1.
∴k的值为﹣1+![]() 或﹣1﹣
或﹣1﹣![]() 或1;
或1;
(3)由“x≥1时函数y随着x的增大而减小”可知,抛物线开口向下,
∴k<0,且对称轴在直线x=1的左侧,
∴﹣![]() ≤1,即
≤1,即![]() ≤1.
≤1.
解不等式组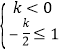 ,
,
解得﹣2≤k<0.

练习册系列答案
相关题目






