Question

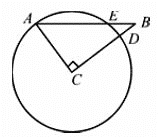
【题目】如图，△ABC中，∠C=Rt∠，AC=6，BC=8，以点C为圆心，CA为半径的圆与AB，BC分别交于点E，D，则BE的长为( )

A. B. C. D.

Answer 1

【答案】A

【解析】

在Rt△ABC中，由勾股定理可直接求得AB的长；过C作CM⊥AB，交AB于点M，由垂径定理可得M为AE的中点，在Rt△ACM中，根据勾股定理得AM的长，从而得到AE的长．

在Rt△ABC中，

∵AC=6，BC=8，

∴AB=10,

过C作CM⊥AB，交AB于点M，如图所示，

由垂径定理可得M为AE的中点，
∵S△ABC=ACBC=ABCM，且AC=6，BC=8，AB=10，

∴CM=,

在Rt△ACM中，根据勾股定理得：AC2=AM2+CM2，即36=AM2+（）2,

解得：AM＝3.6，

AE＝7.2，

所以BE＝AB－AE＝10－7.2＝1.8.

故选A.