题目内容
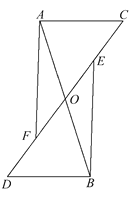
【题目】在平行四边形ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.
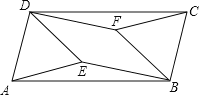
【答案】证明见解析.
【解析】试题分析: 由题意先证∠DAE=∠BCF=60°,再由SAS证△DCF≌△BAE,继而题目得证.
试题解析:
∵四边形ABCD是平行四边形,
∴CD=AB,AD=CB,∠DAB=∠BCD.
又∵△ADE和△BCF都是等边三角形,
∴DE=AD=AE,CF=BF=BC,∠DAE=∠BCF=60°.
∴BF=DE,CF=AE,∠DCF=∠BCD-∠BCF,∠BAE=∠DAB-∠DAE,
即∠DCF=∠BAE.
在△DCF和△BAE中,
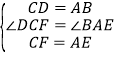
∴△DCF≌△BAE(SAS).
∴DF=BE.
又∵BF=DE,
∴四边形BEDF是平行四边形.

练习册系列答案
相关题目