题目内容
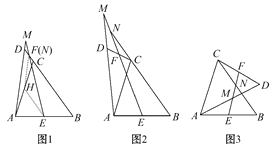
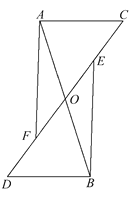
【题目】如图所示,AB,CD交于点O,AC∥DB,AO=BO,E,F分别为OC,OD的中点,连接AF,BE,求证AF∥BE.
【答案】证明见解析.
【解析】
首先连接AE、BF,根据AC∥BD得到∠C=∠D,再根据OA=OB,∠AOC=∠BOD,从而利用AAS证明△AOC≌△BOD;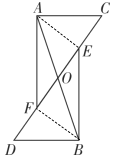
接下来根据全等三角形的性质可得DO=CO,再根据E,F是OC,OD中点得到OE=OF,利用平行四边形的判定与性质即可完成证明.
证明:连接AE、BF.

∵AC∥BD,
∴∠C=∠D.
∵OA=OB,∠AOC=∠BOD,
∴△AOC≌△BOD,
∴CO=DO.
∵E、F分别是OC,OD的中点,
∴EO=FO.
∵AO=BO,EO=FO,
∴四边形AEBF是平行四边形,
∴AF∥BE.

【题目】在东西向的马路上有一个巡岗亭A,巡岗员甲从岗亭A出发以13km/h速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
4 | -5 | 3 | -4 | -3 | 6 | -1 |
(1)求第六次结束时甲的位置(在岗亭A的东边还是西边?距离多远?)
(2)在第几次结束时距岗亭A最远?距离A多远?
(3)巡逻过程中配置无线对讲机,并一直与留守在岗亭A的乙进行通话,问在甲巡逻过程中,甲与乙的保持通话时长共多少小时?
【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.