题目内容
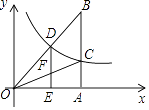
【题目】如图10,在平面直角坐标系中,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,且
,且![]() 满足
满足![]() .现同时将点
.现同时将点![]() 分别向上平移2个单位,再向右平移1个单位,分别得到点
分别向上平移2个单位,再向右平移1个单位,分别得到点![]() 的对应点
的对应点![]() ,连接
,连接![]() 得
得![]() .
.
(1)直接写出点![]() 的坐标和四边形
的坐标和四边形![]() 的面积;
的面积;
(2)若在坐标轴上存在点![]() ,使
,使![]() 四边形
四边形![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)若点![]() 在直线
在直线![]() 上运动,连接
上运动,连接![]() .请画出图形,写出
.请画出图形,写出![]() 的数量关系并证明.
的数量关系并证明.
【答案】(1)![]() ,
,![]() ,8;(2)
,8;(2)![]() 或
或![]() 或
或![]() 或
或![]() ;(3)当点
;(3)当点![]() 在
在![]() 上,
上,![]() ,当点
,当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ,当点
,当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() .画图及证明见解析.
.画图及证明见解析.
【解析】
(1)根据非负数的性质求出a、b的值得出点A、B的坐标,再由平移可得点C、D的坐标,即可知答案;
(2)分点M在x轴和y轴上两种情况,设出坐标,根据S△ACM=S四边形ABDC列出方程求解可得;
(3)分当点![]() 在
在![]() 上、点
上、点![]() 在线段
在线段![]() 的延长线上、和当点
的延长线上、和当点![]() 在线段
在线段![]() 的延长线上时,分别作平行线即可求解.
的延长线上时,分别作平行线即可求解.
(1)由![]() ,得:
,得:![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() ;
;
(2)①![]() 在
在![]() 轴上,设
轴上,设![]() 坐标为
坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]() 或
或![]() ,
,
![]() 点的坐标为
点的坐标为![]() 或
或![]() ;
;
②![]() 在
在![]() 轴上,设点
轴上,设点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]() 或
或![]() ,
,
所以点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
综上所述![]() 点的坐标为
点的坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;
;
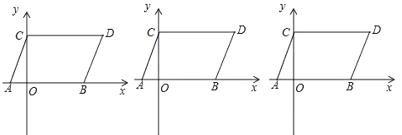
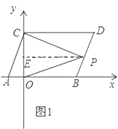
(3)当点![]() 在
在![]() 上,如图1,
上,如图1,
![]() ;
;
理由如下:过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,则
,则
![]() ,
,
![]() ,
,
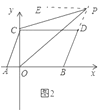
当点![]() 在线段
在线段![]() 的延长线上时,如图2,
的延长线上时,如图2,
![]() ,
,
理由如下:过![]() 点作
点作![]() 交
交![]() 轴于点
轴于点![]() ,则
,则
![]() ,
,
![]() .
.
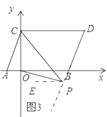
当点![]() 在线段
在线段![]() 的延长线上时,如图3:
的延长线上时,如图3:
![]() ,
,
理由如下:过点![]() 作
作![]() ;则
;则
![]() ,
,
![]() .
.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目