题目内容
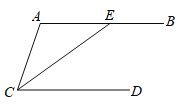
【题目】如图,∠ACE=∠AEC.
(1)若CE平分∠ACD,求证:AB∥CD.
(2)若AB∥CD,求证:CE平分∠ACD.请在(1)、(2)中选择一个进行证明.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据等量代换得到∠ACE=∠AEC,再根据平行线的判定,即可得出AB∥CD;
(2)根据等量代换得到∠ACE=∠ECD,再根据角平分线的定义,即可得出CE平分∠ACD.
解:(1)∵CE平分∠ACD.(已知)
∴∠ACE=∠ECD.(角平线定义)
∵∠ACE=∠AEC.(已知)
∴∠ECD=∠AEC.(等量代换)
∴AB∥CD.(内错角相等,两直线平行)
(2)∵AB∥CD.(已知)
∴∠AEC=∠ECD.(两直线平行,内错角相等)
∵∠ACE=∠AEC.(已知)
∴∠ACE=∠ECD.(等量代换)
∴CE平分∠ACD.

练习册系列答案
相关题目
【题目】在东西向的马路上有一个巡岗亭A,巡岗员甲从岗亭A出发以13km/h速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
4 | -5 | 3 | -4 | -3 | 6 | -1 |
(1)求第六次结束时甲的位置(在岗亭A的东边还是西边?距离多远?)
(2)在第几次结束时距岗亭A最远?距离A多远?
(3)巡逻过程中配置无线对讲机,并一直与留守在岗亭A的乙进行通话,问在甲巡逻过程中,甲与乙的保持通话时长共多少小时?