题目内容
【题目】两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1,固定△ABC不动,将△DEF进行如下操作: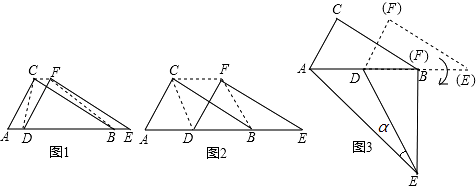
(1)操作发现
如图①,△DEF沿线段AB向右平移(即D点在线段AB内移动),连接DC、CF、FB,四边形CDBF的形状在不断变化,但它的面积不变化,请求出其面积.
(2)猜想论证
如图②,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
(3)拓展研究
如图③,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB的边上,此时F点恰好与B点重合,连接AE,则sinα= .
【答案】
(1)解:如图1,∵△DEF沿线段AB向右平移(即D点在线段AB内移动),
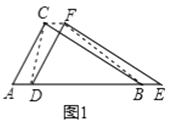
∴CF=AD,AC=DF,
∴四边形ACFD为平行四边形,
∴AD∥CF,
∴S△DCF=S△BCF=S△ACD,
∴S四边形CDBF=S△CDB+S△BCF=S△CDB+S△ACD=S△ACB,
在Rt△ACB中,∵∠A=60°,
∴BC= ![]() AC=
AC= ![]() ,
,
∴S△ABC= ![]() ×1×
×1× ![]() =
= ![]() ,
,
∴S四边形CDBF= ![]()
(2)解:四边形CDBF为菱形.理由如下:
如图2,∵点D为斜边AB的中点,
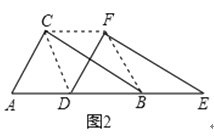
∴DC=DA=DB,
∵CF∥AD,CF=AD,
∴CF=BD,CF∥DB,
∴四边形CDBF为平行四边形,
而DC=DB,
∴四边形CDBF为菱形;
(3)![]()
【解析】解:(3)作DH⊥AE于H,如图,
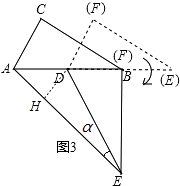
在Rt△ACB中,∵∠A=60°,
∴AB=2AC=2,
∵点D为AB的中点,
∴AD=BD= ![]() AB=1,
AB=1,
∵绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,
∴∠EFD=90°,EB= ![]() ,DE=AB=2,
,DE=AB=2,
在Rt△ABE中,AE= ![]() =
= ![]() =
= ![]() ,
,
∵ ![]() DHAB=
DHAB= ![]() ADEB,
ADEB,
∴DH= ![]() =
= ![]() ,
,
在Rt△EDH中,sinα= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】掌握平移的性质和锐角三角函数的定义是解答本题的根本,需要知道①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

【题目】在东西向的马路上有一个巡岗亭A,巡岗员甲从岗亭A出发以13km/h速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
4 | -5 | 3 | -4 | -3 | 6 | -1 |
(1)求第六次结束时甲的位置(在岗亭A的东边还是西边?距离多远?)
(2)在第几次结束时距岗亭A最远?距离A多远?
(3)巡逻过程中配置无线对讲机,并一直与留守在岗亭A的乙进行通话,问在甲巡逻过程中,甲与乙的保持通话时长共多少小时?
【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.