题目内容
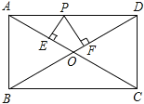
【题目】如图,矩形ABCD的两边AB=3,BC=4,P是AD上任一点,PE⊥AC于点E,PF⊥BD于点F.求PE+PF的值.
【答案】![]()
【解析】
首先连接OP.由矩形ABCD的两边AB=3,BC=4,可求得OA=OD=![]() ,S△AOD=
,S△AOD=![]() S矩形ABCD然后由S△AOD=S△AOP+S△DOP=
S矩形ABCD然后由S△AOD=S△AOP+S△DOP=![]() OAPE+
OAPE+![]() ODPF=
ODPF=![]() OA(PE+PF)=
OA(PE+PF)=![]() ×(PE+PF)=3,求得答案.
×(PE+PF)=3,求得答案.
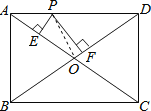
解:连接OP,
∵矩形ABCD的两边AB=3,BC=4,
∴S矩形ABCD=ABBC=12,OA=OC,OB=OD,AC=BD,AC=![]() =5,
=5,
∴S△AOD=![]() S矩形ABCD=3,OA=OD=
S矩形ABCD=3,OA=OD=![]() ,
,
∵PE⊥AC, PF⊥BD
∴S△AOD=S△AOP+S△DOP=![]() OAPE+
OAPE+![]() ODPF=
ODPF=![]() OA(PE+PF)=
OA(PE+PF)=![]() ×(PE+PF)=3,
×(PE+PF)=3,
∴PE+PF=![]() .
.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
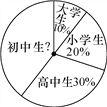
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.