题目内容
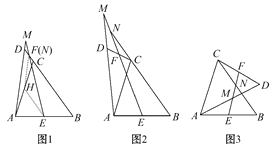
【题目】如图,已知AB=AD,AC=AE,∠BAD=∠CAE=90°,试判断CD与BE的大小关系和位置关系,并进行证明.
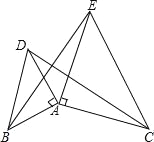
【答案】CD=BE,CD⊥BE.
【解析】
利用等腰直角三角形的性质和全等三角形的判定定理可得△BAE≌△DAC,由全等三角形的性质可得BE=DC,∠BEA=∠DCA,设AE与CD相交于点F,易得
∠BEA+∠DFE=90°.即CD⊥BE.
解:CD=BE,CD⊥BE,
理由如下:
因为∠BAD=∠CAE=90°,所以∠BAD+∠DAE=∠CAE+∠DAE,
即∠BAE=∠DAC.
因为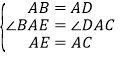 ,
,
所以△BAE≌△DAC(SAS).
所以BE=DC,∠BEA=∠DCA.
如图,设AE与CD相交于点F,因为∠ACF+∠AFC=90°,∠AFC=∠DFE,
所以∠BEA+∠DFE=90°.即CD⊥BE.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目