Question

【题目】在平面直角坐标系xOy中，已知A（﹣1，5），B（4，2），C（﹣1，0）三点．
（1）点A关于原点O的对称点A′的坐标为 ， 点B关于x轴的对称点B′的坐标为 ， 点C关于y轴的对称点C的坐标为 ．
（2）求（1）中的△A′B′C′的面积．

Answer 1

【答案】
（1）（1，﹣5）；（4，﹣2）；（1，0）
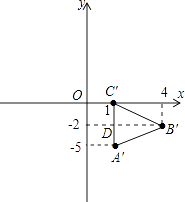
（2）解：如图，∵A′（1，﹣5），B′（4，﹣2），C′（1，0）．

∴A′C′=|﹣5﹣0|=5，B′D=|4﹣1|=3，

∴S△A′B′C′= A′C′B′D= ×5×3=7.5，即（1）中的△A′B′C′的面积是7.5．

【解析】解：（1）∵A（﹣1，5）， ∴点A关于原点O的对称点A′的坐标为（1，﹣5）．
∵B（4，2），
∴点B关于x轴的对称点B′的坐标为（4，﹣2）．
∵C（﹣1，0），
∴点C关于y轴的对称点C′的坐标为（1，0）．
所以答案是：（1，﹣5），（4，﹣2），（1，0）．
【考点精析】解答此题的关键在于理解三角形的面积的相关知识，掌握三角形的面积=1/2×底×高，以及对关于原点对称的点的坐标的理解，了解两个点关于原点对称时，它们的坐标的符号相反，即点P（x，y）关于原点的对称点为P’（-x，-y）．