Question

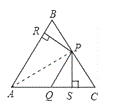
【题目】如图，在△ABC中，∠BAC=108°，EF、MN分别是AB、AC的垂直平分线，点E、N在BC上，则∠EAN等于( )

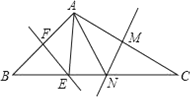
A. 72°B. 54°C. 36°D. 18°

Answer 1

【答案】C

【解析】

先由∠BAC=108°及三角形内角和定理求出∠B+∠C的度数，再根据线段垂直平分线的性质求出∠B=∠BAE，∠C=∠CAN，即∠B+∠C=∠BAE+∠CAN，由∠EAN=∠BAC-（∠BAE+∠CAN）解答即可．

∵△ABC中，∠BAC=108°，

∴∠B+∠C=180°-∠BAC=180°-108°=72°，

∵EF、MN分别是AB、AC的中垂线，

∴∠B=∠BAE，∠C=∠CAN，

即∠B+∠C=∠BAE+∠CAN=72°，

∴∠EAN=∠BAC-（∠BAE+∠CAN）=108°-72°=36°．

故答案为：C.