题目内容
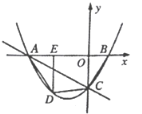
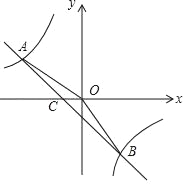
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于二象限内的A点和四象限内的B点,与x轴将于点C,连接AO,已知AO=2
的图象交于二象限内的A点和四象限内的B点,与x轴将于点C,连接AO,已知AO=2![]() ,tan∠AOC=
,tan∠AOC=![]() ,点B的坐标为(a,﹣4).
,点B的坐标为(a,﹣4).
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△AOB的面积.
【答案】(1)y=﹣![]() ,y=﹣x﹣2;(2)﹣4<x<0或x>2;(3)S△AOB=6.
,y=﹣x﹣2;(2)﹣4<x<0或x>2;(3)S△AOB=6.
【解析】
(1)先根据AO=2![]() ,tan∠AOC=
,tan∠AOC=![]() 求得点A的坐标,代入反比例函数解析式求得m的值,继而得出点B的坐标,根据点A、B坐标可得一次函数解析式;
求得点A的坐标,代入反比例函数解析式求得m的值,继而得出点B的坐标,根据点A、B坐标可得一次函数解析式;
(2)由函数图象找到直线位于双曲线下方所对应的x的范围即可得;
(3)先求得点C坐标,再根据S△AOB=S△AOC+S△BOC求解可得.
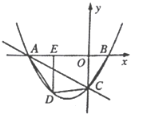
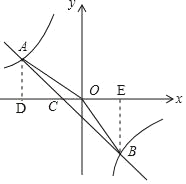
(1)如图,作AD⊥x轴于点D,
∵tan∠AOC=![]() =
=![]() ,
,
∴设AD=a、则OD=2a,
∴AO=![]() ,
,
则a=2,
∴AD=2、OD=4,
则点A坐标为(﹣4,2),
将点A坐标代入y=![]() ,得:m=﹣8,
,得:m=﹣8,
∴反比例函数解析式为y=﹣![]() ,
,
将点B(a,﹣4)代入y=﹣![]() ,得:a=2,
,得:a=2,
∴B(2,﹣4),
将点A、B坐标代入y=kx+b,
得:![]() ,
,
解得:![]() ,
,
则一次函数解析式为y=﹣x﹣2;
(2)由函数图象知当﹣4<x<0或x>2时,一次函数的值小于反比例函数的值;
(3)在y=﹣x﹣2中当y=0时,﹣x﹣2=0,
解得:x=﹣2,
∴OC=2,
S△AOB=S△AOC+S△BOC
=![]() OCAD+
OCAD+![]() OCBE
OCBE
=![]() ×2×2+
×2×2+![]() ×2×4
×2×4
=2+4
=6.

练习册系列答案
相关题目