题目内容
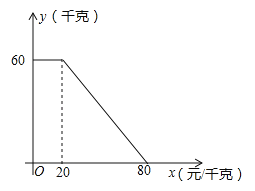
【题目】某商店以20元/千克的单价新进一批商品，经调查发现，在一段时间内，销售量y（千克）与销售单价x（元/千克）之间为一次函数关系，如图所示．
（1）求y与x的函数表达式；
（2）要使销售利润达到800元，销售单价应定为每千克多少元？
【答案】（1）
；（2）40元或60元．
【解析】试题（1）当20≤x≤80时，利用待定系数法即可得到y与x的函数表达式；
（2）根据销售利润达到800元，可得方程（x﹣20）（﹣x+80）=800，解方程即可得到销售单价．
试题解析：解：（1）当0＜x＜20时，y=60；
当20≤x≤80时，设y与x的函数表达式为y=kx+b，把（20，60），（80，0）代入，可得： 
，解得： 
，∴y=﹣x+80，∴y与x的函数表达式为
；
（2）若销售利润达到800元，则（x﹣20）（﹣x+80）=800，解得x1=40，x2=60，∴要使销售利润达到800元，销售单价应定为每千克40元或60元．
练习册系列答案
相关题目
【题目】某校积极参与垃圾分类活动，以班级为单位收集可回收的垃圾，下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图（每组含前一个边界值，不含后一个边界值）.
某校七年级各班一周收集的可回收垃圾的质量频数表
组别（kg） | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
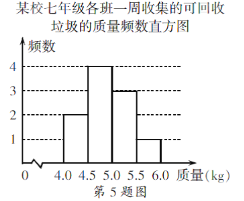
（1）求a的值；
（2）已知收集的可回收垃圾以0.8元/kg被回收，该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.
