题目内容
【题目】一个正多边形的对称轴共有10条，且该正多边形的半径等于4，那么该正多边形的边长等于____．
【答案】2
.
【解析】
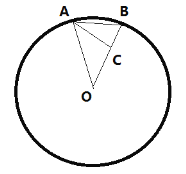
根据题意作图，由一个正多边形的对称轴共有10条，可知这个正多边形为正十边形，故每个内角为144°，则图中∠OAB=∠OBA=72°，故∠AOB=36°，在BO上找一点C，使AC=CO，可证得△ACO、△ABC都为等腰三角形.故∠BAC=∠AOB=36°，故可得△ABO∽△BCA，设AB=x，可知OC=x，BC=4-x，再根据相似三角形的性质即可求解.
根据题意作图，∵一个正多边形的对称轴共有10条，
∴这个正多边形为正十边形，故每个内角为144°，
则图中∠OAB=∠OBA=72°，
故∠AOB=36°，
在BO上找一点C，使AC=CO，则∠OAC=∠AOB=36°，∠BAC=∠OAB-∠OAC=36°，
∴∠ACB=180°-∠CAB-∠ABC=72°.
∴△ACO、△ABC都为等腰三角形.
∵∠BAC=∠AOB=36°，
∴△ABO∽△BCA，
设AB=x，可知OC=x，BC=4-x，
∴
，即
解得x=2
.(- 2舍去)
则正多边形的边长2
练习册系列答案
阅读快车系列答案
相关题目
