题目内容
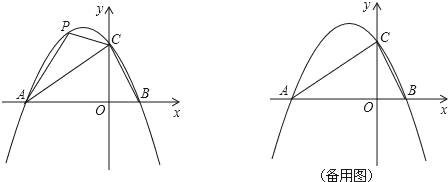
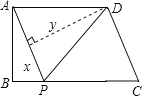
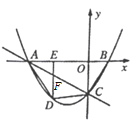
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,经过点
,经过点![]() 的抛物线
的抛物线![]() 与
与![]() 轴的另一个交点为点
轴的另一个交点为点![]() ,点
,点![]() 是抛物线上一点,过点
是抛物线上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
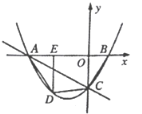
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当点
当点![]() 在第三象限,设
在第三象限,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;
的坐标;
![]() 连接
连接![]() ,若
,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 存在最大值,最大值为
存在最大值,最大值为![]() ,此时点D的坐标为
,此时点D的坐标为![]() ; (3)点
; (3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)先利用一次函数求出点A的坐标,再用待定系数法即可求出抛物线的解析式;
(2)先用含m的式子表示出点D的坐标及DF的长,进而求出![]() 与
与![]() 的函数关系式,根据顶点式即可得出答案;
的函数关系式,根据顶点式即可得出答案;
(3)由题可知△ OBC与△ EAD相似,根据根据的性质即可得出答案.
解:(1)在![]() 中,令
中,令![]() ,得
,得![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
将点![]() ,
,![]() 代入
代入![]() 中,得,
中,得,
![]() ,
,
解得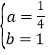 ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
(2)如图,设![]() 交直线
交直线![]() 于点
于点![]() ,
,
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 抛物线开口向下,
抛物线开口向下,
![]() 当
当![]() 时,
时,![]() 存在最大值,最大值为
存在最大值,最大值为![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 此时点
此时点![]() 的坐标为
的坐标为![]() ;
;
(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目