题目内容
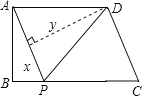
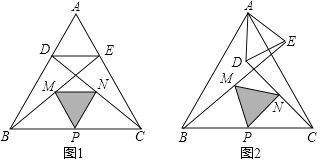
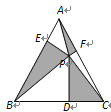
【题目】如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=![]() ,那么△ABC的内切圆半径为___
,那么△ABC的内切圆半径为___
【答案】![]()
【解析】
过P点作正△ABC的三边的平行线,可得△MPN,△OPQ,△RSP都是正三角形,四边形ASPM,四边形NCOP,四边形PQBR是平行四边形,则可得黑色部分的面积=白色部分的面积,进而求出三角形ABC的面积,然后求出等边三角形的边长和高,再根据等边三角形的内切圆的半径等于高的三分之一即可求出半径的长度.
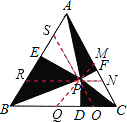
如图,过P点作正△ABC的三边的平行线,
则△MPN,△OPQ,△RSP都是正三角形,
四边形ASPM,四边形NCOP,四边形PQBR是平行四边形,
故可知黑色部分的面积=白色部分的面积,
∵S△APF+S△BPE+S△PCD=![]() ,
,
∴S△ABC=![]() ,
,
∵S△ABC=![]() AB2sin60°=
AB2sin60°=![]() ,
,
∴AB=6,
∴三角形ABC的高h=3![]() ,
,
则△ABC的内切圆半径r=![]() h=
h=![]() .
.
故答案为:![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg) | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
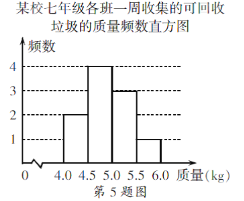
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.