题目内容
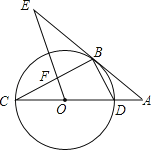
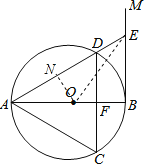
【题目】如图,![]() 是
是![]() 的直径,过点
的直径,过点![]() 作
作![]() 的切线
的切线![]() ,弦
,弦![]() ,交
,交![]() 于点
于点![]() ,且弧
,且弧![]() 弧
弧![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() 是等边三角形;
是等边三角形;
(2)若![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)见解析;(2)2![]() .
.
【解析】
(1)由AB是⊙O的直径,BM是⊙O的切线,得到AB⊥BE,由于CD∥BE,得到CD⊥AB,根据垂径定理得到弧![]() 弧
弧![]() ,于是得到弧
,于是得到弧![]() 弧
弧![]() =弧AC ,问题即可得证;
=弧AC ,问题即可得证;
(2)连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,得到∠DAC=60°又直角三角形的性质得到BE=![]() AE,ON=
AE,ON=![]() AO,设⊙O的半径为:r则ON=
AO,设⊙O的半径为:r则ON=![]() r,AN=DN=
r,AN=DN=![]() r,由于得到EN=2+
r,由于得到EN=2+![]() r,BE=
r,BE=![]() AE=
AE=![]() ,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
(1)证明:∵AB是⊙O的直径,BM是⊙O的切线,
∴AB⊥BE,
∵CD∥BE,
∴CD⊥AB,
∴弧AD=弧AC,
∵弧![]() 弧
弧![]() ,
,
∴弧![]() 弧
弧![]() =弧AC,
=弧AC,
∴AD=AC=CD,
∴△ACD是等边三角形;
(2)解:连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,
∴∠DAC=60°
∵AD=AC,CD⊥AB,
∴∠DAB=30°,
∴BE=![]() AE,ON=
AE,ON=![]() AO,
AO,
设⊙O的半径为:r,
∴ON=![]() r,AN=DN=
r,AN=DN=![]() r,
r,
∴EN=2+![]() r,BE=
r,BE=![]() AE=
AE=![]() ,
,
在Rt△NEO与Rt△BEO中,
OE2=ON2+NE2=OB2+BE2,
即(![]() )2+(2+
)2+(2+![]() )2=r2+(
)2=r2+(![]() )2,
)2,
∴r=2![]() ,
,
∴OE2=(![]() )2+25=28,
)2+25=28,
∴OE=2![]() .
.

【题目】已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/kg)的变化而变化,具体变化规律如表所示:
销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
月销售量y(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
(1)请根据上表,写出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)若该绿茶的月销售利润为w(元),且售单价得高于80元,求w与x之间的函数关系式,并求出x为何值时,w的值最大?
(3)已知商家经销一种绿茶,用于装修门面已投资3000元,在第一个月,按使w获得最大值的销售单价进行销售后;在第二个月受物价部门干预,销售单价不得高于78元,要想在全部收回装修投资的基础上使这两个月的总利润至少达到1722元,求第二个月的销售单价的取值范围?