题目内容
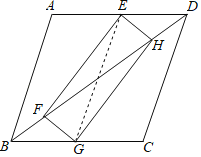
【题目】如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．
（1）求证：BG=DE；
（2）若E为AD中点，FH=2，求菱形ABCD的周长．
【答案】(1)详见解析；(2)8
【解析】
（1）先根据矩形的性质、平行线的性质得出
，再根据邻补角的定义可得
，又根据菱形的性质、平行线的性质可得
，最后根据三角形全等的判定定理与性质即可得证；
（2）如图，连接EG，先根据矩形的性质可得EG的长，再根据中点的性质、菱形的性质、题（1）的结论可得四边形ABGE是平行四边形，从而可得AB的长，然后根据菱形的周长公式即可得．
（1）∵四边形EFGH是矩形
∵四边形ABCD是菱形
在
和
中，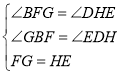
；
（2）如图，连接EG
∵四边形EFGH是矩形，
∵四边形ABCD是菱形
∵E为AD中点
∴四边形ABGE是平行四边形
∴菱形ABCD的周长为
故菱形ABCD的周长为8．
练习册系列答案
阅读快车系列答案
相关题目
