Question

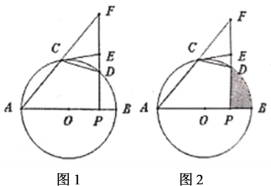
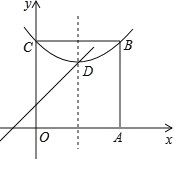
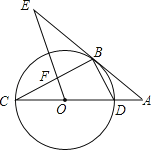
【题目】如图，CD是⊙O的直径，点B在⊙O上，连接BC、BD，直线AB与CD的延长线相交于点A，AB2＝ADAC，OE∥BD交直线AB于点E，OE与BC相交于点F．

（1）求证：直线AE是⊙O的切线；

（2）若⊙O的半径为3，cosA＝，求OF的长．

Answer 1

【答案】（1）详见解析；（2）．

【解析】

（1）连接OB，根据已知条件得到△ABD∽△ACB，再根据相似三角形的性质得到∠ABD＝∠ACB，由等腰三角形的性质得到∠OBC＝∠ACB，等量代换得到∠OBC＝∠ABD，于是得到结论；

（2）设AB＝4x，OA＝5x，根据勾股定理得到AB＝4，OA＝5，求得AD＝2，根据平行线分相等成比例定理得到BE＝6，由勾股定理得到OE＝＝3，根据三角形的面积公式得到BF＝，根据三角函数的定义即可得到结论．

（1）

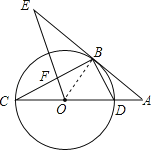
如图，连接OB，

∵AB2＝ADAC，

∴，

∵∠A＝∠A，

∴△ABD∽△ACB，

∴∠ABD＝∠ACB，

∵OB＝OC，

∴∠OBC＝∠ACB，

∴∠OBC＝∠ABD，

∵CD是⊙O的直径，

∴∠CBD＝90°，

∴∠OBC+∠OBD＝90°，∠OBD+∠ABD＝90°，

即∠OBA＝90°，

∴直线AE是⊙O的切线；

（2）∵OB＝3，cosA＝，

∴设AB＝4x，OA＝5x，

∵OA2＝AB2+OB2，

∴（5x）2＝（4x）2+32，

∴x＝1，

∴AB＝4，OA＝5，

∴AD＝2，

∵OE∥BD，

∴，

∴BE＝6，

∴OE＝＝3，

∵∠CBD＝90°，BD∥OE，

∴∠EFB＝90°，

∵S△OBE＝OBBE＝OEBF，

∴OBBE＝OEBF，

∴BF＝，

∵tan∠E＝，

∴EF，

∴OF＝OE﹣EF＝．