题目内容
【题目】某高铁站已于几年前投入使用,计划在广场内种植![]() 两种花木共10500棵,若
两种花木共10500棵,若![]() 花木数量比
花木数量比![]() 花木数量的一半多1500棵.
花木数量的一半多1500棵.
(1)![]() 两种花木的数量分别是多少棵?
两种花木的数量分别是多少棵?
(2)如果园林处安排27人同时种植这两种花木,每人每天能种植![]() 花木50棵或
花木50棵或![]() 花木30棵,应分别安排多少人种植
花木30棵,应分别安排多少人种植![]() 花木和
花木和![]() 花木,才能确保同时完成各自的任务?
花木,才能确保同时完成各自的任务?
【答案】(1)![]() 花木的数量是6000棵,
花木的数量是6000棵,![]() 花木的数量是4500棵;(2)安排12人种植
花木的数量是4500棵;(2)安排12人种植![]() 花木,15人种植
花木,15人种植![]() 花木,才能确保同时完成各自的任务.
花木,才能确保同时完成各自的任务.
【解析】
(1)根据在广场内种植A,B两种花木共10500棵,若B花木数量是A花木数量的一半多1500棵,可以列出相应的二元一次方程组,从而可以解答本题;
(2)根据题意可以列出相应的分式方程,从而可以解答本题,最后要检验.
解:(1)设![]() 花木的数量是
花木的数量是![]() 棵,
棵,![]() 花木的数量是
花木的数量是![]() 棵.
棵.
根据题意,得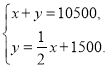
解得![]()
答:![]() 花木的数量是6000棵,
花木的数量是6000棵,![]() 花木的数量是4500棵.
花木的数量是4500棵.
(2)设安排![]() 人种植
人种植![]() 花木,则安排
花木,则安排![]() 人种植
人种植![]() 花木根据题意,得
花木根据题意,得![]() ,
,
解得![]() ,
,
经检验,![]() 是原方程的解,
是原方程的解,
![]() (人).
(人).
答:安排12人种植![]() 花木,15人种植
花木,15人种植![]() 花木,才能确保同时完成各自的任务.
花木,才能确保同时完成各自的任务.

【题目】涌泉镇是中国无核蜜桔之乡,已知某蜜桔种植大户冯大爷的蜜桔成本为2元/千克,如果在未来90天蜜桔的销售单价p(元/千克)与时间t(天)之间的函数关系式为p=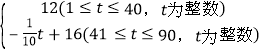 ,且蜜桔的日销量y(千克)与时间t(天)满足一次函数关系,其部分数据如下表所示:
,且蜜桔的日销量y(千克)与时间t(天)满足一次函数关系,其部分数据如下表所示:
时间t/天 | 1 | 10 | 20 | 40 | 70 | 90 |
日销售量y/千克 | 105 | 150 | 200 | 300 | 450 | 550 |
(1)求y与t之间的函数表达式;
(2)在未来90天的销售中,预测哪一天的日销售利润最大?最大日销售利润为多少元?
(3)在实际销售的后50天中,冯大爷决定每销售1千克蜜桔就捐赠n元利润(n<5)给留守儿童作为助学金,销售过程中冯大爷发现,恰好从第51天开始,和前一天相比,扣除捐赠后的日销售利润逐日减少,请求出n的取值范围.