题目内容
【题目】矩形![]() 中,
中,![]() (其中
(其中![]() )
)
(1)点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ;
;
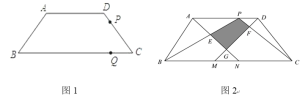
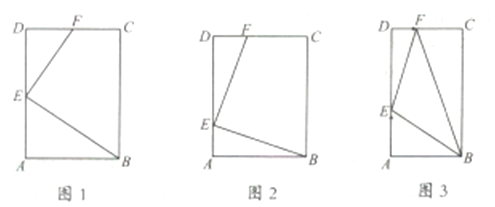
①如图![]() ,若
,若![]() ,且点
,且点![]() 是
是![]() 中点,求证
中点,求证![]() ;
;
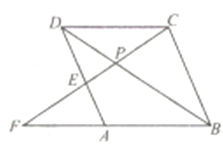
②如图![]() ,若
,若![]() ,且
,且![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,当
,当![]() ,
,![]() 时,点
时,点![]() 以
以![]() 的速度从
的速度从![]() 到
到![]() ,点
,点![]() 以
以![]() 的速度从
的速度从![]() 到
到![]() ,当点
,当点![]() 到
到![]() 时两点都停止运动,则点
时两点都停止运动,则点![]() 的运动时间
的运动时间![]() 为多少时,
为多少时,![]() 的面积
的面积![]() 最小,最小面积为多少?
最小,最小面积为多少?
【答案】(1)①证明见解析;②证明见解析;(2)点![]() 的运动时间为
的运动时间为![]() 秒时,
秒时,![]() 的面积最小,且最小面积为
的面积最小,且最小面积为![]() .
.
【解析】
(1)①证明![]() ,证明CF=DF=
,证明CF=DF=![]() ,证得CF=DF;
,证得CF=DF;
②由![]() 得,
得,![]() ,得
,得![]() ,结合
,结合![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,证得BC=2CF;
,证得BC=2CF;
(2)表示出AE,DE,DF,CF,得出![]() =
=![]() ,可得面积最小值.
,可得面积最小值.
解:(1)①![]() 是
是![]() 的中点
的中点
∴![]()
∵![]()
∴![]()
令![]()
则![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
又∵![]()
∴![]()
∴![]() ,即
,即![]()
解得![]()
∵![]()
∵![]()
∴![]()
∵![]()
②由![]() 得,
得,![]()
∴![]()
又∵![]()
∴![]() ,
,![]()
∵![]()
令![]() ,则
,则![]()
∴![]()
∴![]()
∴![]()
故![]()
(3)![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() =
=![]() =
=![]()
(其中![]() )
)
抛物线![]() 的图象开口向上
的图象开口向上
顶点为![]()
∵![]()
∴当![]() 时,
时,![]() 有最小值,且最小值为
有最小值,且最小值为![]()
即点![]() 的运动时间为
的运动时间为![]() 秒时,
秒时,![]() 的面积最小,且最小面积为
的面积最小,且最小面积为![]() .
.

练习册系列答案
相关题目