题目内容
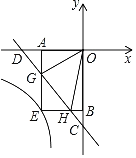
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=![]() 的解析式为_____.
的解析式为_____.
【答案】y=![]()
【解析】
过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,设点A(-![]() ,0)则AO=
,0)则AO=![]() ,DO=2,AD=2-
,DO=2,AD=2-![]() ,由“AAS”可证△GAO≌△PNG,可得NP=AG=2-
,由“AAS”可证△GAO≌△PNG,可得NP=AG=2-![]() ,AO=GN=
,AO=GN=![]() ,可求点P坐标,求出一次函数解析式,可求点H的纵坐标,即可求解.
,可求点P坐标,求出一次函数解析式,可求点H的纵坐标,即可求解.
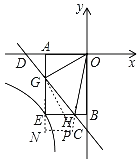
解:如图,过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,
设点A(-![]() ,0)
,0)
∴AO=![]() ,
,
∵直线y=﹣x﹣2与x轴,y轴分别交于点D,C,
∴点D(﹣2,0),∠ADC=45°,
∴DO=2,AD=2﹣![]() ,
,
∵AE⊥OD,
∴∠ADG=∠AGD=45°,
∴AD=AG=2﹣![]() ,
,
∵GP⊥GO,∠GOH=45°,
∴∠GPO=∠GOP=45°,
∴GP=GO,
∵∠AGO+∠AOG=90°,∠AGO+∠NGP=90°,
∴∠AOG=∠NGP,
又∵∠GNP=∠GAO=90°,GO=GP,
∴△GAO≌△PNG(AAS),
∴NP=AG=2﹣![]() ,AO=GN=
,AO=GN=![]() ,
,
∴AN=2,
∴点P(2﹣2![]() ,﹣2),
,﹣2),
∴直线OP解析式为:y=![]() x,
x,
联立方程组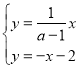
∴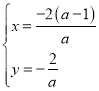
∴点H的纵坐标为![]() ,
,
∴点E(![]() ,
,![]() )
)
∵反比例函数y=![]() 的图象过点E,
的图象过点E,
∴k=![]() ×(
×(![]() )=2,
)=2,
∴反比例函数解析式为:y=![]() ,
,
故答案为:y=![]() .
.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.