题目内容
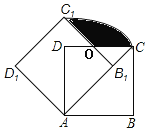
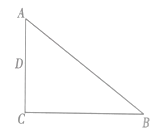
【题目】如图，在边长为
的正方形ABCD中，点E，F是对角线AC的三等分点，点P在正方形的边上，则满足PE+PF=
的点P的个数是（ ）
A.0B.4C.8D.16
【答案】B
【解析】
作点F关于BC的对称点M，连接EM交BC于点P，则PE+PF的最小值为EM，由对称性可得CM=5，∠BCM=45°，根据勾股定理得EM=
，进而即可得到结论．
作点F关于BC的对称点M，连接EM交BC于点P，则PE+PF的最小值为EM．
∵正方形ABCD中，边长为
，
∴AC=×
=15，
∵点E，F是对角线AC的三等分点，
∴EC=10，FC=AE=5，
∵点M与点F关于BC对称，
∴CF=CM=5，∠ACB=∠BCM=45°，
∴∠ACM=90°，
∴EM=
，
∴在BC边上，只有一个点P满足PE+PF=，
同理：在AB，AD，CD边上都存在一个点P，满足PE+PF=，
∴满足PE+PF=的点P的个数是4个．
故选B．
【题目】某文具商店销售学习用品，已知某品牌钢笔的进价是20元，销售过程发现，每月销量y支与销售单价x元（x为正整数）之间满足一次函数关系，且每支钢笔的售价不低于进价，也不高于35元，下表是y与x之间的对应数据：
销售单价x（元） | … | 22 | 24 | 30 | … |
月销量y（只） | … | 92 | 84 | 60 | … |
（1）求y与x的函数关系式并直接写出自变量x的取值范围.
（2）每支钢笔的售价定为多少元时，月销售利润恰为600元？
（3）每支钢笔的售价定为多少元时可使月销售利润最大？最大的月利润是多少？
【题目】小明和小红为了更直观了解“物体质量”的概念，各选五个鸡蛋称重，以每个
为标准，大于或等于即为达标，超过标准部分的克数记为正数，不足标准部分的克数记为负数．小明所统计的数据为实际称重读数，小红为记录数据，把所得数据整理成如下统计表（单位：
）．
序号 数据 姓名 | 1 | 2 | 3 | 4 | 5 |
小明 | 48 | 50 |
| 49 | 51 |
小红 |
|
|
| 2 | 1 |
经过统计发现，小明所选鸡蛋质量的平均数为
，小红所选鸡蛋质量的众数为
，根据以上信息：
（1）填空：
，
；
（2）通过计算说明，小明和小红哪个选取的鸡蛋大小更均匀，请说明理由；
（3）现从小明和小红所选取的鸡蛋里各随机挑一个，这两个鸡蛋质量都达标的概率是多少？
