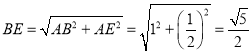题目内容
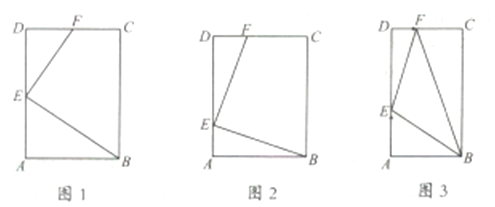
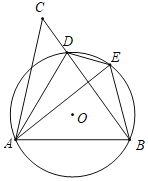
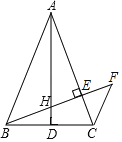
【题目】如图,在△ABC中,AB=AC,AD是边BC上的中线,BE⊥AC于点E,交AD于点H过点C作CF∥AB交BE的延长线于点F.
(1)求证:△ABH∽△BFC;
(2)求证:BH2=HEHF;
(3)若AB=2,∠BAC=45°,求BH的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据两角对应相等两三角形相似证明即可;
(2)连接CH,首先证明BH=HC,再证明△CHE∽△FHC可得结论;
(3)延长CH交AB于M,由题意CM⊥AB.利用全等三角形的性质证明AM=AE=2,求出BM即可解决问题.
(1)证明:∵AB=AC,AD是边BC上的中线,
∴∠BAD=∠CAD,AD⊥BC,
∵BE⊥AC,
∴∠BDH=∠AEH=90°,
∵∠AHE=∠BHD,
∴∠DBH=∠DAC=∠BAD,
∵CF∥AB,
∴∠ABH=∠F,
∴△ABH∽△BFC;
(2)连接CH.∵AD⊥BC,BD=DC,
∴BH=HC,
∴∠HBC=∠HCB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABH=∠ACH,
∵CF∥AB,
∴∠ABH=∠F,
∴∠HCE=∠F,
∵∠CHE=∠CHF,
∴△CHE∽△FHC,
∴![]() ,
,
∴HC2=HEHF,
∵BH=HC,
∴BH2=HEHF;
(3)延长CH交AB于M,由题意CM⊥AB,

∵BE⊥AC,∠BAC=45°,
∴∠ABE=45°,
∴AE=ABcos45°=2×![]() =
=![]() ,
,
∵∠HAM=∠HAE,∠HMA=∠HEA,∠AMH=∠AEH=90°,
∴△AHM≌△AHE(AAS),
∴AM=AE=![]() ,
,
∴BM=AB﹣AM=2﹣![]() ,
,
在Rt△BHM中,BH=![]() =2
=2![]() ﹣2.
﹣2.

练习册系列答案
相关题目