ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§Εΰ¥ΈΚ· ΐyΘΫaΘ®x2+2mx©¹3m2Θ©Θ®Τδ÷–aΘ§m «≥Θ ΐaΘΦ0Θ§mΘΨ0Θ©ΒΡΆΦœσ”κx÷αΖ÷±πΫΜ”ΎAΓΔBΘ®ΒψAΈΜ”ΎΒψBΒΡ”“≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ®0Θ§3Θ©Θ§ΒψD‘ΎΕΰ¥ΈΚ· ΐΒΡΆΦœσ…œΘ§CDΓΈABΘ§Ν§ΫαADΘ°ΙΐΒψAΉς…δœΏAEΫΜΕΰ¥ΈΚ· ΐΒΡΆΦœσ”ΎΒψEΘ§ABΤΫΖ÷ΓœDAEΘ°
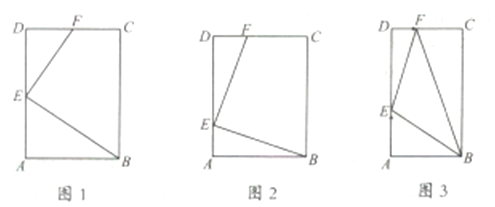
Θ®1Θ©«σa”κmΒΡΙΊœΒ ΫΘΜ
Θ®2Θ©«σ÷ΛΘΚ![]() ΈΣΕ®÷ΒΘΜ
ΈΣΕ®÷ΒΘΜ
Θ®3Θ©…ηΗΟΕΰ¥ΈΚ· ΐΒΡΆΦœσΒΡΕΞΒψΈΣFΘ°ΧΫΥςΘΚ‘Ύx÷αΒΡ’ΐΑκ÷α…œ «Ζώ¥φ‘ΎΒψGΘ§Ν§ΫαGFΘ§“‘œΏΕΈGFΓΔADΓΔAEΒΡ≥ΛΕ»ΈΣ»ΐ±Ώ≥ΛΒΡ»ΐΫ«–Έ «÷±Ϋ«»ΐΫ«–ΈΘΩ»γΙϊ¥φ‘ΎΘ§÷Μ“Σ’“≥ω“ΜΗω¬ζΉψ“Σ«σΒΡΒψGΦ¥Ω…Θ§≤Δ”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ ΨΗΟΒψΒΡΚαΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
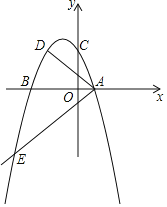
ΓΨ¥πΑΗΓΩΘ®1Θ©am2ΘΫ©¹1ΘΜΘ®2Θ©÷ΛΟςΦϊΫβΈωΘΜΘ®3Θ©¥φ‘ΎΘ§ΒψGΒΡΚαΉχ±ξΈΣ3mΘ°
ΓΨΫβΈωΓΩ
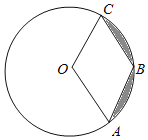
Θ®1Θ©ΫΪΒψCΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏ±μ¥ο ΫΘ§Φ¥Ω…«σΫβΘΜ
Θ®2Θ©÷ΛΟςRtADMΓςΓΉRtΓςANEΘ§«σ≥ωΒψEΘ®xΘ§![]() Θ©Θ§ΫΪΒψEΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏ±μ¥ο ΫΘ§ΒΟΒΫEΘ®©¹4mΘ§©¹5Θ©Θ§Φ¥Ω…«σΫβΘΜ
Θ©Θ§ΫΪΒψEΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏ±μ¥ο ΫΘ§ΒΟΒΫEΘ®©¹4mΘ§©¹5Θ©Θ§Φ¥Ω…«σΫβΘΜ
Θ®3Θ©«σ≥ωΒψFΘ®©¹mΘ§4Θ©Θ§ΒΟΒΫ÷±œΏFCΒΡ±μ¥ο ΫΘ§«σ≥ωΒψGΘ®3mΘ§0Θ©Θ§Φ¥Ω…«σΫβΘ°
ΫβΘΚΘ®1Θ©ΫΪΒψCΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏ±μ¥ο ΫΒΟΘΚ©¹3am2ΘΫ3Θ§
ΫβΒΟΘΚam2ΘΫ©¹1ΘΜ
Θ®2Θ©Ε‘”ΎΕΰ¥ΈΚ· ΐyΘΫaΘ®x2+2mx©¹3m2Θ©Θ§ΝνyΘΫ0Θ§‘ρxΘΫmΜρ©¹3mΘ§
ΓύΚ· ΐΒΡΕ‘≥Τ÷αΈΣΘΚxΘΫ©¹mΘ§
ÿCDøABȧ
ΓύΒψDΓΔCΒΡΉίΉχ±ξœύΆ§Θ§Ι ΒψDΘ®©¹2mΘ§3Θ©Θ§
Ι ΒψAΓΔBΒΡΉχ±ξΖ÷±πΈΣΘΚΘ®mΘ§0Θ©ΓΔΘ®©¹3mΘ§0Θ©Θ§
…ηΒψEΘ®xΘ§yΘ©Θ§yΘΫaΘ®x2+2mx©¹3m2Θ©Θ§
Ζ÷±πΙΐΒψDΓΔEΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΖ÷±πΈΣMΓΔNΘ§
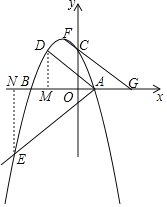
ΓΏABΤΫΖ÷ΓœDAEΘ§
ΓύΓœDAMΘΫΓœEANΘ§
ΓύRtADMΓςΓΉRtΓςANEΘ§
Γύ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§
Θ§
ΫβΒΟΘΚyΘΫ![]() Θ§
Θ§
Ι ΒψEΘ®xΘ§![]() Θ©Θ§
Θ©Θ§
ΫΪΒψEΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏ±μ¥ο Ϋ≤ΔΫβΒΟΘΚxΘΫ©¹4mΘ§
‘ρyΘΫ![]() ΘΫ©¹5Θ§
ΘΫ©¹5Θ§
Ι ΒψEΘ®©¹4mΘ§©¹5Θ©Θ§
Ι ![]() ΘΫ
ΘΫ![]() ΘΫ
ΘΫ![]() ΈΣΕ®÷ΒΘΜ
ΈΣΕ®÷ΒΘΜ
Θ®3Θ©¥φ‘ΎΘ§άμ”…ΘΚ
Κ· ΐΒΡΕ‘≥Τ÷αΈΣxΘΫ©¹mΘ§Β±xΘΫ©¹m ±Θ§yΘΫaΘ®x2+2mx©¹3m2Θ©ΘΫ4Θ§Φ¥ΒψFΘ®©¹mΘ§4Θ©Θ§
”…ΒψFΓΔCΒΡΉχ±ξΒΟΘ§÷±œΏFCΒΡ±μ¥ο ΫΈΣΘΚyΘΫ©¹![]() x+3Θ§ΝνyΘΫ0Θ§‘ρxΘΫ3mΘ§Φ¥ΒψGΘ®3mΘ§0Θ©Θ§
x+3Θ§ΝνyΘΫ0Θ§‘ρxΘΫ3mΘ§Φ¥ΒψGΘ®3mΘ§0Θ©Θ§
GF2ΘΫΘ®3m+mΘ©2+42ΘΫ16m2+16Θ§
Ά§άμAD2ΘΫ9m2+9Θ§AE2ΘΫ25m2+25Θ§
Ι AE2ΘΫAD2+GF2Θ§
GFΓΔADΓΔAEΒΡ≥ΛΕ»ΈΣ»ΐ±Ώ≥ΛΒΡ»ΐΫ«–Έ «÷±Ϋ«»ΐΫ«–ΈΘ§
ΒψGΒΡΚαΉχ±ξΈΣ3mΘ°

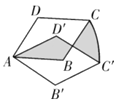
ΓΨΧβΡΩΓΩ”–ΦΉΓΔ““ΝΫΦ“≤ίί°≤…’Σ‘ΑΘ§≤ίί°ΒΡœζ έΦέΗώœύΦδΘ§‘Ύ…ζ≥ΛΆζΦΨΘ§ΝΫΦ“Ψυ≈≈≥ω”≈ΜίΖΫΑΗ.ΦΉ‘ΑΒΡ”≈ΜίΖΫΑΗ «:≤…’ΣΒΡ≤ίί°≤Μ≥§Ιΐ![]() ±Θ§Α¥‘≠Φέœζ έΘΜ»τ≥§Ιΐ
±Θ§Α¥‘≠Φέœζ έΘΜ»τ≥§Ιΐ![]() ≥§Ιΐ≤ΩΖ÷
≥§Ιΐ≤ΩΖ÷![]() ’έ”≈ΜίΘΜ““‘ΑΒΡ”≈ΜίΖΫΑΗ «:”ΈΩΆΫχ‘Α–ηΙΚ¬ρ
’έ”≈ΜίΘΜ““‘ΑΒΡ”≈ΜίΖΫΑΗ «:”ΈΩΆΫχ‘Α–ηΙΚ¬ρ![]() ‘ΣΟ≈Τ±.≤…’ΣΒΡ≤ίί°÷±Ϋ”Α¥ΫΒΦέ≥ω έ.“―÷Σ‘ΎΦΉ‘ΑΓΔ““‘Α≤…’Σ≤ίί°
‘ΣΟ≈Τ±.≤…’ΣΒΡ≤ίί°÷±Ϋ”Α¥ΫΒΦέ≥ω έ.“―÷Σ‘ΎΦΉ‘ΑΓΔ““‘Α≤…’Σ≤ίί°![]() ±Θ§Υυ–ηΖ―”ΟœύΆ§.
±Θ§Υυ–ηΖ―”ΟœύΆ§.
‘Ύ““≤…’Σ‘ΑΥυ–ηΖ―”Ο![]() ( ‘Σ)”κ≤ίΟΖ≤…’ΣΝΩ
( ‘Σ)”κ≤ίΟΖ≤…’ΣΝΩ![]() («ßΩΥ)¬ζΉψ“Μ¥ΈΚ· ΐΙΊœΒΘ§»γœ¬±μ:
(«ßΩΥ)¬ζΉψ“Μ¥ΈΚ· ΐΙΊœΒΘ§»γœ¬±μ:
ΐΝΩ |
|
|
|
| ΓΛΓΛΓΛ |
Ζ―”Ο |
|
|
|
| ΓΛΓΛΓΛ |
Θ®1Θ©«σ![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ Ϋ(≤Μ±Ί–¥≥ω
ΒΡΚ· ΐΙΊœΒ Ϋ(≤Μ±Ί–¥≥ω![]() ΒΡΖΕΈß)ΘΜ
ΒΡΖΕΈß)ΘΜ
Θ®2Θ©«σΝΫΗω≤…’Σ‘ΑΒΡ≤ίί°‘Ύ…ζ≥ΛΆζΦΨ«ΑΒΡœζ έΦέΗώ.≤Δ«σ‘ΎΦΉ≤…’Σ‘ΑΥυ–ηΖ―”Ο![]() (‘Σ)”κ≤ίί°≤…’ΣΝΩ
(‘Σ)”κ≤ίί°≤…’ΣΝΩ![]() («ßΩΥ)ΒΡΚ· ΐΙΊœΒ Ϋ
(«ßΩΥ)ΒΡΚ· ΐΙΊœΒ Ϋ![]() ΘΜ
ΘΜ
Θ®3Θ©»τΦΈγςΉΦ±ΗΜ®Ζ―![]() ‘Σ»Ξ≤…’Σ≤ίί°Θ§»ΞΡΡΗω‘Α≤…’ΣΘ§Ω…“‘ΒΟΒΫΗϋΕύ ΐΝΩΒΡ≤ίί°ΘΩ ΥΒΟςάμ”….
‘Σ»Ξ≤…’Σ≤ίί°Θ§»ΞΡΡΗω‘Α≤…’ΣΘ§Ω…“‘ΒΟΒΫΗϋΕύ ΐΝΩΒΡ≤ίί°ΘΩ ΥΒΟςάμ”….