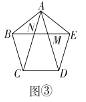
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线,经过
的平分线,经过![]() 两点的圆的圆心
两点的圆的圆心![]() 恰好落在
恰好落在![]() 上,
上,![]() 分别与
分别与![]() 交于点
交于点![]() .若
.若![]() .则图中阴影部分的面积为( )
.则图中阴影部分的面积为( )
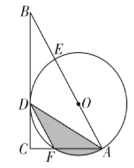
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
连接OD,OF.首先证明OD∥AC,推出S阴=S扇形OFA,再证明△AOF是等边三角形即可解决问题.
连接OD,OF.
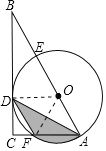
∵AD是∠BAC的平分线,
∴∠DAB=∠DAC,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠ODA=∠DAC,
∴OD∥AC,
∴∠ODB=∠C=90°,
∴S△AFD=S△OFA,
∴S阴=S扇形OFA,
∵OD=OA=2,AB=6,
∴OB=4,
∴OB=2OD,
∴∠B=30°,
∴∠A=60°,
∵OF=OA,
∴△AOF是等边三角形,
∴∠AOF=60°,
∴S阴=S扇形OFA ![]() .
.
故选:C.

【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.